[머신러닝] 비지도 학습 : K-Means Clustering (Iris dataset 군집화)

K-Means Clustering

https://upload.wikimedia.org/wikipedia/commons/b/b3/K-means_versus_k-medoids.png
중심점(Centroid) 기반의 클러스터링
데이터는 다른 군집의 중심점보다 속한 군집의 중심점에 가까워야 한다.
방법
1. 초기 세팅
클러스터 개수(K) 설정: 사용자는 클러스터의 개수를 결정해야 한다.
초기 중심 설정: K개의 클러스터의 중심을 초기에 무작위로 설정한다.
2. 할당 단계
각 데이터 포인트를 가장 가까운 중심에 할당. 이 때 거리 측정은 일반적으로 유클리디안 거리를 사용합.
각 데이터 포인트는 그것과 가장 가까운 클러스터에 속하게 된다.
3. 업데이트 단계
각 클러스터의 중심을 해당 클러스터에 속한 데이터 포인트들의 평균 위치로 이동시킨다.
4. 반복
할당 단계와 업데이트 단계를 반복하면서 중심의 위치가 변하지 않을 때까지 클러스터링을 진행
일반적으로 클러스터 중심점의 위치 변화가 임계값 T 이하일 때 까지 반복하는 방식을 사용한다.
장점
직관적이고 구현이 간단하다.
단점
K에 따라 성능이 크게 좌우된다.
초기값에 따라 Local Minimum에 빠질 수 있음 -> Convex하지 않는 데이터에 성능이 좋지 않다.
초기 세팅
데이터 수집 : 사용할 데이터를 수집하고 전처리한다.
from sklearn.datasets import load_iris
from matplotlib import pyplot as plt
import numpy as np
idata = load_iris()
print(dir(idata))
print(idata.data.shape)
print(idata.feature_names)
print(idata.target) #라벨
print(idata.target_names)
X = idata.data
y = idata.target
n = X.shape[0]
# Feature 4가지
w = X[:,0]
x = X[:,1]
y = X[:,2]
z = X[:,3]
plt.scatter(w, x, alpha=0.5)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.show()
plt.scatter(y, z, alpha=0.5)
plt.xlabel('petal length( (cm))')
plt.ylabel('petal width (cm)')
plt.show()
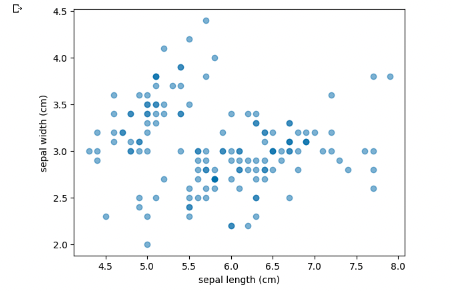
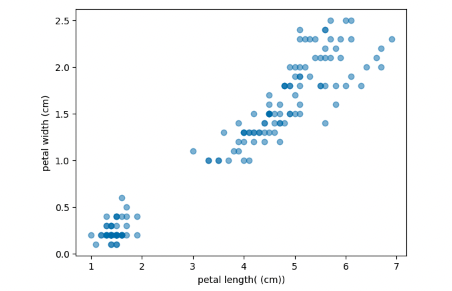
군집화 할 때 가장 많이 예제로 쓰이는 붓꽃 군집화 문제이다. 붓꽃 데이터는 4가지의 특징으로 구성되며,각각 꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비를 나타낸다. 붓꽃은 결국 3가지의 종류로 클러스터링된다고 한다.
w, x, y, z는 데이터셋의 특성을 나타내는 배열이다.
클러스터 개수(K) 설정 / 초기 중심 설정
import numpy as np
k = 3
centroids_w = np.random.uniform(min(w), max(w), k)
centroids_x = np.random.uniform(min(x), max(x), k)
centroids_y = np.random.uniform(min(y), max(y), k)
centroids_z = np.random.uniform(min(z), max(z), k)
centroids = list(zip(centroids_w, centroids_x, centroids_y, centroids_z)) #중심점 4개
centroids = np.array(centroids)각각의 4가지 Feature 대해서 3개의 K를 설정하여 군집화를 진행할 것이다.
from copy import deepcopy
labels = np.zeros(n)
points = np.array(list(zip(w,x,y,z)))
centroids_old = np.zeros(centroids.shape) #Before Centroid
error = np.zeros(k) #Current Error
error_old = deepcopy(error) #Before Error업데이트 단계에서 비교될 직전 중심점(Centroid)를 담아둘 변수와, 오차를 계산하기 위해서 두 가지 변수를 생성해주었다.
유클리드 거리를 구하는 함수 작성
def distance(a, b):
alen = len(a)
sum = 0
for aidx in range (alen):
sum += (a[aidx] - b[aidx]) ** 2
return sum ** 0.5K-Means에서 거리 기준으로 자주 사용되는 유클리드 거리를 구하는 코드를 작성해주었다.
Centroid 할당 및 업데이트 반복
for i in range(k):
error[i] = distance(centroids_old[i], centroids[i]) #Centroid의 거리 차이
idx = 0
while(error.any() != 0):
# cluster input points to the nearest centroid
for i in range(n): #각 point들
distances = np.zeros(k) #k=3, [0,0,0]
for j in range(k):
distances[j] = distance(points[i], centroids[j])
labels[i] = np.argmin(distances) #point의 최소 distance centroid
# compute new centroids from clusters
centroids_old = deepcopy(centroids)
for i in range(k): #각 centroid들
point = []
for j in range(n):
if(labels[j] == i):
point.append(points[j])
centroids[i] = np.mean(point, axis=0) #평균 Point로 Centroid 이동
error_old = error
for j in range(k):
error[j] = distance(centroids_old[j], centroids[j]) #Centroid의 거리 차이
print(idx, "times error:", error)
idx += 1
print("Centroids", centroids)
데이터를 군집화하고 중심점을 업데이트하는 과정을 반복하는 부분이다.
데이터를 초기 중심점으로 시작하여 데이터를 군집화하고 중심점을 업데이트하는 과정을 반복함으로써 군집화를 수행하고 있다.
초기화된 중심점(centroid)과 이전 중심점 사이의 거리를 계산하여 error 배열에 저장한다. 이는 중심점의 변화 값을 나타낸다.
오차(error)가 0이 될 때까지 반복문을 실행한다. 이는 중심점이 더 이상 변하지 않을 때까지 군집화 과정을 반복한다.
첫 번째 for 반복문에서는 각 데이터 포인트를 가장 가까운 Centroid에 할당한다. 즉, 각 데이터 포인트에 대해 Centroid의 클러스터 레이블(labels)로 업데이트 시키는 과정이다.
두 번째 for 반복문에서는 각 클러스터 내의 포인트들의 평균을 계산하여 포인트들의 중심으로 Centroid를 이동시킨다.
또한 Centroid의 변화를 측정하기 위해 이전 중심점과 현재 중심점 사이의 거리를 계산하여 error 배열에 업데이트한다.

결과로는 배열에 저장된 최종 중심점과 오차를 출력한다.
Scikit-Learn 이용
from sklearn.cluster import KMeans
model = KMeans(n_clusters = 3)
model.fit(points)
print(idata.target)
print(model.labels_)
cnt = 0
for i in range(len(idata.target)):
cnt += (idata.target[i] == model.labels_[i])
print(cnt / len(idata.target))
Scikitlearn 라이브러리는 K-Means 또한 내장되어 있다.
비교적 간단하게 모델을 이용하여 학습시킬 수 있다.
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 앙상블 모델 : Voting / Bagging / Random Forest 적용해보기 (0) | 2023.08.30 |
|---|---|
| [머신러닝] 비지도 학습 : 연관 규칙 분석 / 차원 축소 (0) | 2023.08.30 |
| [머신러닝] 비지도 학습 : 군집화(Clustering) (0) | 2023.08.28 |
| [머신러닝] 지도 학습 : 분류(Classification)와 모델 평가 (0) | 2023.08.28 |
| [인공지능] AI 모델의 검증 기준과 검증 방법 (1) | 2023.08.28 |













