[머신러닝] 지도 학습 : 분류(Classification)와 모델 평가

포스팅된 글의 인용한 모든 이미지는 CCL 라이선스의 이미지만을 사용했으며, 출처를 밝힙니다.
분류 (Classification)

분류는 지도 학습의 방법 중 하나이다.
- 범주형 변수를 인식하고 구분하는 방법
- 데이터를 잘 구분하는 경계(Decision Boundary)를 찾는 문제.
로지스틱 회귀와 분류

- 결정 경계 문제를 해결하기 위해 로지스틱 분류를 가장 많이 사용
- 로지스틱(시그모이드) 함수는 x->∞일 시 1, x->(-∞)일 시 0, x=0일 때 변곡점, 좌우대칭, 증가함수의 특징을 가진다.
로지스틱 분류의 손실 함수의 조건
기존의 MSE Loss 함수는 로지스틱 함수를 제곱하고 미분하기에 어려움
-> Cross Entropy Loss 함수를 손실 함수로 사용한다.
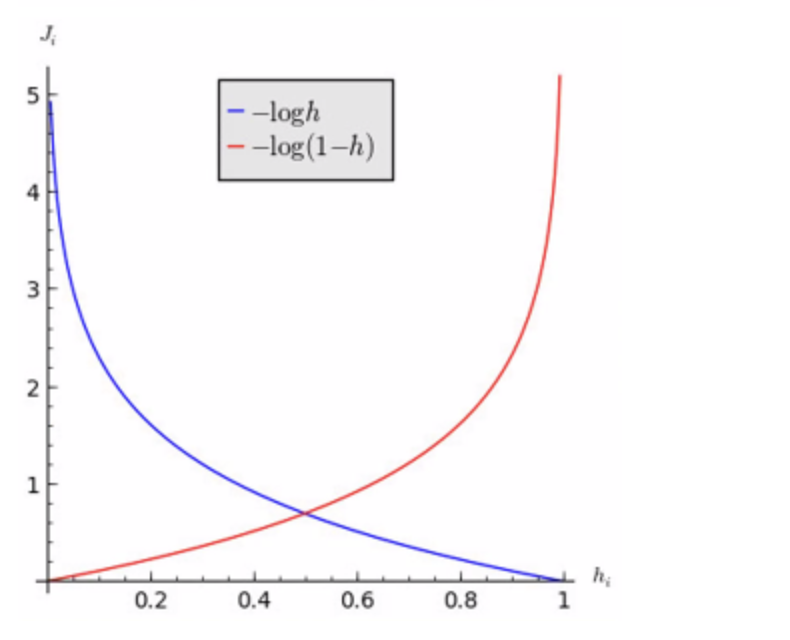
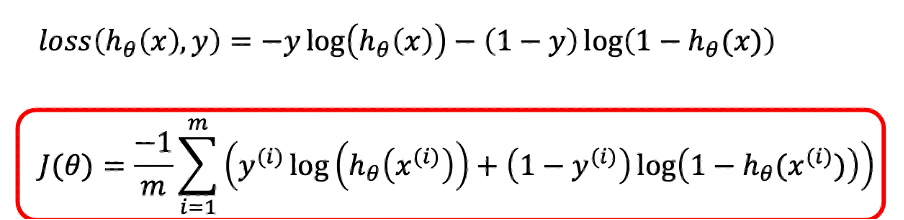
- Convex한 함수 -> Gradient Descent의 적용이 쉬움, Local Minimum 문제 X
- 미분이 쉬운 함수 -> Log함수나 시그모이드 함수
- Loss함수 = loss(hθ(x), y)의 hθ(x)가 0 또는 1만 가지는 성질
- Y = 1일 때, hθ(x) = 1이면 0, hθ(x) = 0이면 ∞
- Y = 0일 때, hθ(x) = 0이면 0, hθ(x) = 1이면 ∞
- 정답을 맞추지 못할 경우, Loss는 매우 크고 맞출 경우 Loss는 없음
로지스틱 회귀의 손실 함수의 미분의 의미 = 분포의 차이 -> 이를 최소화하는게 목표
엔트로피란 불규칙성, 정보의 분포를 의미한다.
서포트 벡터 (Support Vector Machine)
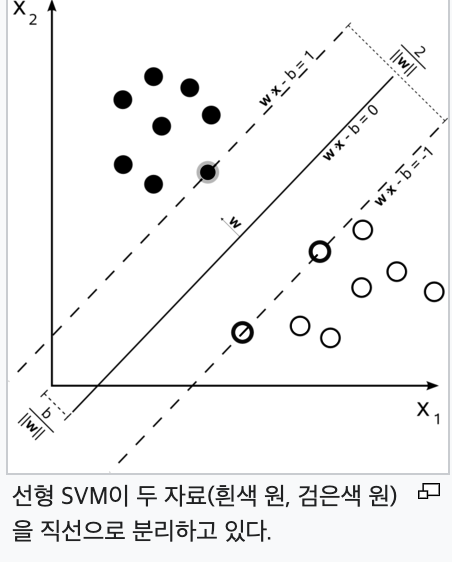
- 이진 분류된 데이터들 사이의 최대 마진을 보장
- 데이터 포인트들 중 일부를 서포트 벡터로 선택한다. 서포트 벡터는 결정 경계와 가장 가까운 데이터 포인트들을 의미한다.
- 서포트 벡터들과 Decision Boundary의 거리를 최대화하여, 최적의 결정 경계를 찾는 것이 목표이다.
SVM의 주요 아이디어는 데이터 포인트들을 나누는 결정 경계를 찾을 때, 가능한 한 클래스들 간의 간격(마진)을 최대화하는 것이다. 분류된 데이터들이 결정 경계로부터 최대한 멀리 떨어져 있을 가능성이 높아진다.
의사 결정 트리(Decesion Tree)
모든 Non-Leaf Node는 2개의 자식 노드를 가짐 : 각 분기 노드는 두 개의 자식 노드로 나뉘어집니다. 이로 인해 트리의 구조는 이진 트리 형태를 띄게 된다.
Root Node (루트 노드): 의사 결정 트리의 시작점, 데이터를 분류하는 과정이 이곳에서 시작
Branch Node (분기 노드): 하나의 특성 또는 기준에 따라 두 개의 경로로 나뉘어지는 노드. 각 경로는 다음 분기노드나 리프노드로 이어짐
Leaf Node (리프 노드): 분류 작업이 끝나고 최종 결과가 나타나는 노드. 하나의 클래스 레이블로 결정
의사 결정 트리(분류)의 생성 원칙
의사 결정 트리를 생성할 때는 다음 주요 원칙들을 고려한다.
분화 추진
의사 결정 트리는 정보 획득을 최대화하는 방향으로 데이터를 분할한다. 정보 획득은 데이터를 분할했을 때 얻을 수 있는 정보의 양을 나타내며, 무질서도(Entropy)의 감소로 표현한다. 정보 획득이 높을수록 데이터의 분류가 더 명확해지며, 이를 통해 더 정확한 Decision Boundary를 찾을 수 있다.
분화 제어
트리가 깊어질수록 발생할 수 있는 Overfitting을 방지하기 위해 트리의 깊이를 제한하거나, 미리 정한 오차 기준을 만족하는 경우에만 더 분기하도록 한다.
정보 획득
정보 획득은 데이터의 무질서도(Entropy) 변화를 기반으로 한다.
엔트로피는 데이터가 얼마나 무질서한지를 나타내는 지표로, 정보 획득은 부모 노드와 자식 노드 간의 엔트로피 차이로 정의되며, 이 값이 클수록 분류가 더 명확해진다는 의미입니다.
분류 모델의 평가
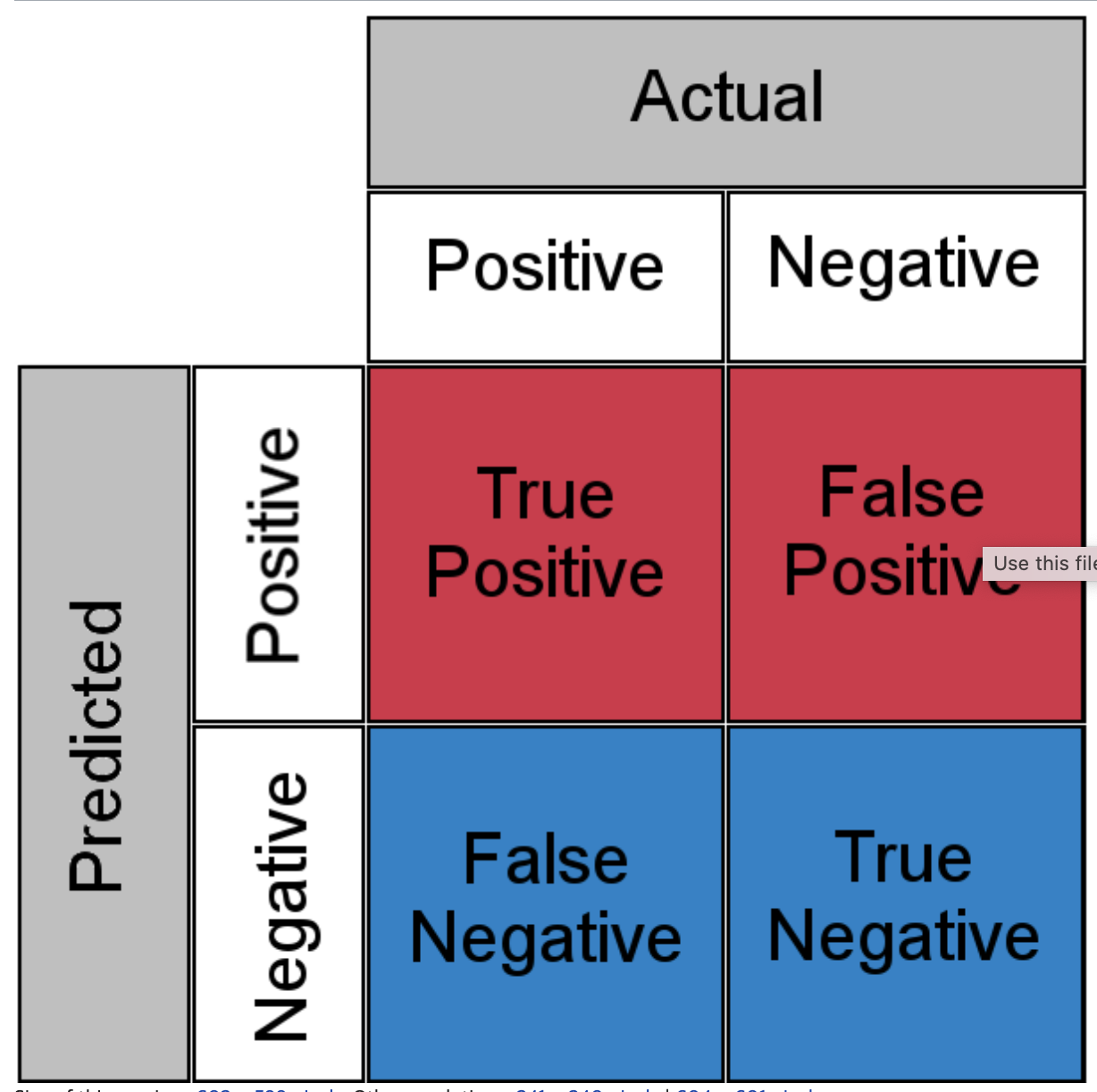
Confusion Matrix
Confusio Matrix, 혼동 행렬은 분류 모델의 성능을 평가하기 위해 사용된다. 실제 클래스와 예측 클래스 간의 관계를 나타내며, 주로 이진 분류에서의 다양한 성능 지표를 계산하는 데 활용한다.
예측 결과를 TP(True Positive), TN(True Negative), FP(False Positive), FN(False Negative)로 나누어서 표현한다.
TP (True Positive): 실제로 Positive한 클래스를 Positive로 정확하게 예측한 경우
TN (True Negative): 실제로 Negative한 클래스를 Negative로 정확하게 예측한 경우
FP (False Positive): 실제로 Negative한 클래스를 Positive로 잘못 예측한 경우
FN (False Negative): 실제로 Positive한 클래스를 Negative로 잘못 예측한 경우
1. Precision (정밀도)
Precision은 모델이 Positive로 예측한 것 중에서 실제로 Positive한 비율을 나타내는 지표. 즉, 모델이 Positive로 예측한 것 중에서 얼마나 정확한지를 나타낸다.
Precision = TP / (TP + FP)
2. Recall (재현율 또는 민감도)
Recall은 실제로 Positive한 클래스 중에서 모델이 Positive로 예측한 비율을 나타내는 지표. 모델이 실제 Positive한 경우를 얼마나 잘 찾아내는지를 나타낸다.
Recall = TP / (TP + FN)
3. F1 Score
F1 Score는 Precision과 Recall의 조화평균. 모델의 성능을 종합적으로 평가하는 지표.
F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 비지도 학습 : K-Means Clustering (Iris dataset 군집화) (0) | 2023.08.28 |
|---|---|
| [머신러닝] 비지도 학습 : 군집화(Clustering) (0) | 2023.08.28 |
| [인공지능] AI 모델의 검증 기준과 검증 방법 (1) | 2023.08.28 |
| [머신러닝] 지도 학습 : 다변량 회귀와 경사하강법 최적화 방법(Optimizer) (0) | 2023.05.03 |
| [인공지능] AI 개요와 라이프사이클 (0) | 2023.05.03 |













