[머신러닝] 비지도 학습 : 군집화(Clustering)

포스팅된 글의 인용한 모든 이미지는 CCL 라이선스의 이미지만을 사용했으며, 출처를 밝힙니다.
비지도 학습
- Label이 없는 데이터를 학습시키는 방법
- 유사성을 기반으로 그룹화하거나 데이터에 숨어있는 구조를 파악
비지도 학습의 종류
- 군집화 : 데이터로부터 몇 개의 대표적인 집합을 얻어내는 방법
- 연관 규칙 분석 : 항목들 사이의 관계를 분석하여 연관성을 찾는 방법
- 차원 축소 : 높은 차원의 데이터를 낮은 차원의 데이터로 변환하는 방법
군집화
비지도 학습, 범주형 변수 예측
군집화는 분류와 달리 라벨(카테고리)를 회귀하는 것이 아니라 유사 집단으로 묶는 것
분할적 군집화
- Top-Down, 몇 개의 집합으로 분할할지 결정한 후 유사한 데이터를 모음
- K-Means : 중심점 기반
- DBSCAN : 밀도 기반
- Fuzzy Clustering : 확률 기반
- SOM(Self Organizing Map) : 그래프 기반
계층적 군집화
- Bottom-Up, 유사한 성질의 데이터를 우선 모아서 여러 집합으로 분할함
- 데이터의 유사성을 판단하는 알고리즘을 적용하여 연결하는 방식
- 합병적 군집화 : 상향식 접근 방법, 가장 가까운 데이터 클러스터부터 시작하여 더 큰 클러스터로 병합해 나가면서 진행
* 덴드로그램 : 계층적 군집화의 결과를 시각적으로 표현
K-Means Clustering

중심점(Centroid) 기반의 클러스터링
데이터는 다른 군집의 중심점보다 속한 군집의 중심점에 가까워야 한다.
방법
1. 초기 세팅
클러스터 개수(K) 설정: 사용자는 클러스터의 개수를 결정해야 한다.
초기 중심 설정: K개의 클러스터의 중심을 초기에 무작위로 설정한다.
2. 할당 단계
각 데이터 포인트를 가장 가까운 중심에 할당. 이 때 거리 측정은 일반적으로 유클리디안 거리를 사용합.
각 데이터 포인트는 그것과 가장 가까운 클러스터에 속하게 된다.
3. 업데이트 단계
각 클러스터의 중심을 해당 클러스터에 속한 데이터 포인트들의 평균 위치로 이동시킨다.
4. 반복
할당 단계와 업데이트 단계를 반복하면서 중심의 위치가 변하지 않을 때까지 클러스터링을 진행
일반적으로 클러스터 중심점의 위치 변화가 임계값 T 이하일 때 까지 반복하는 방식을 사용한다.
장점
직관적이고 구현이 간단하다.
단점
K에 따라 성능이 크게 좌우된다.
초기값에 따라 Local Minimum에 빠질 수 있음 -> Convex하지 않는 데이터에 성능이 좋지 않다.
DBSCAN
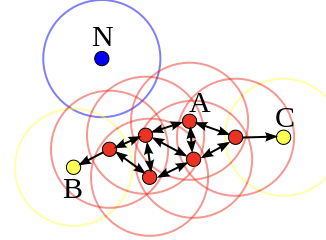
밀도 기반의 클러스터링.
포인트를 아래와 같이 분류
- Core Point : 클러스터에 가장 가까움. 특정 반경(ε) 내에 최소 기준(k)를 만족하 는 점이 존재
- Density Reachable Point : 코어 포인트의 친구. 코어 포인트로부터 특정 반경(ε) 내에 존재
- Density Connected Point : 코어 포인트의 친구의 친구. 코어 포인트로부터 특정 반경(ε) 내에 존재하는 점들의 Path가 존재
- Noise Point : 특정 반경 내에 어떤 점도 존재하지 않음
Core Point(특정 반경(ε) 내에 최소 기준(k)를 만족하는 점)으로부터 특정 반경 내에 존재하는 점들을 루프를 따라 확산시키며 클러스터링하는 방식
장점
클러스터 개수 자동결정, Outlier 발견가능
단점
연산이 오래걸림, 뚜렷한 경계가 없는 데이터에 한계
Fuzzy Clustering
1. 퍼지 알고리즘을 접목하여 확률론적으로 그룹에 속할지 아닐지를 판단하는 방식
2. 속한다/속하지 않는다(0과 1)이 아닌 속할 확률(0~1)로 표현하는 것이 특징
3. FCM (Fuzzy C-Means)는 K-Means와 비슷한 원리로 작동하지만, 포인트를 클러스터에 할당할 때, 하나의 Centroid가 아닌, 각 Centroid에 대해 속하는 정도를 확률적으로 나타낸다. -> 데이터 포인트가 여러 클러스터에 동시에 속할 수 있음
SOM
신경망 기반의 군집화 알고리즘. -> Edge와 Weight를 갱신해가면서 가는 알고리즘
이웃한 그리드 셀들 간의 데이터를 이동시키며 학습한다. -> 비슷한 특성을 가진 데이터가 가까운 셀에 모이게 됨
덴드로그램
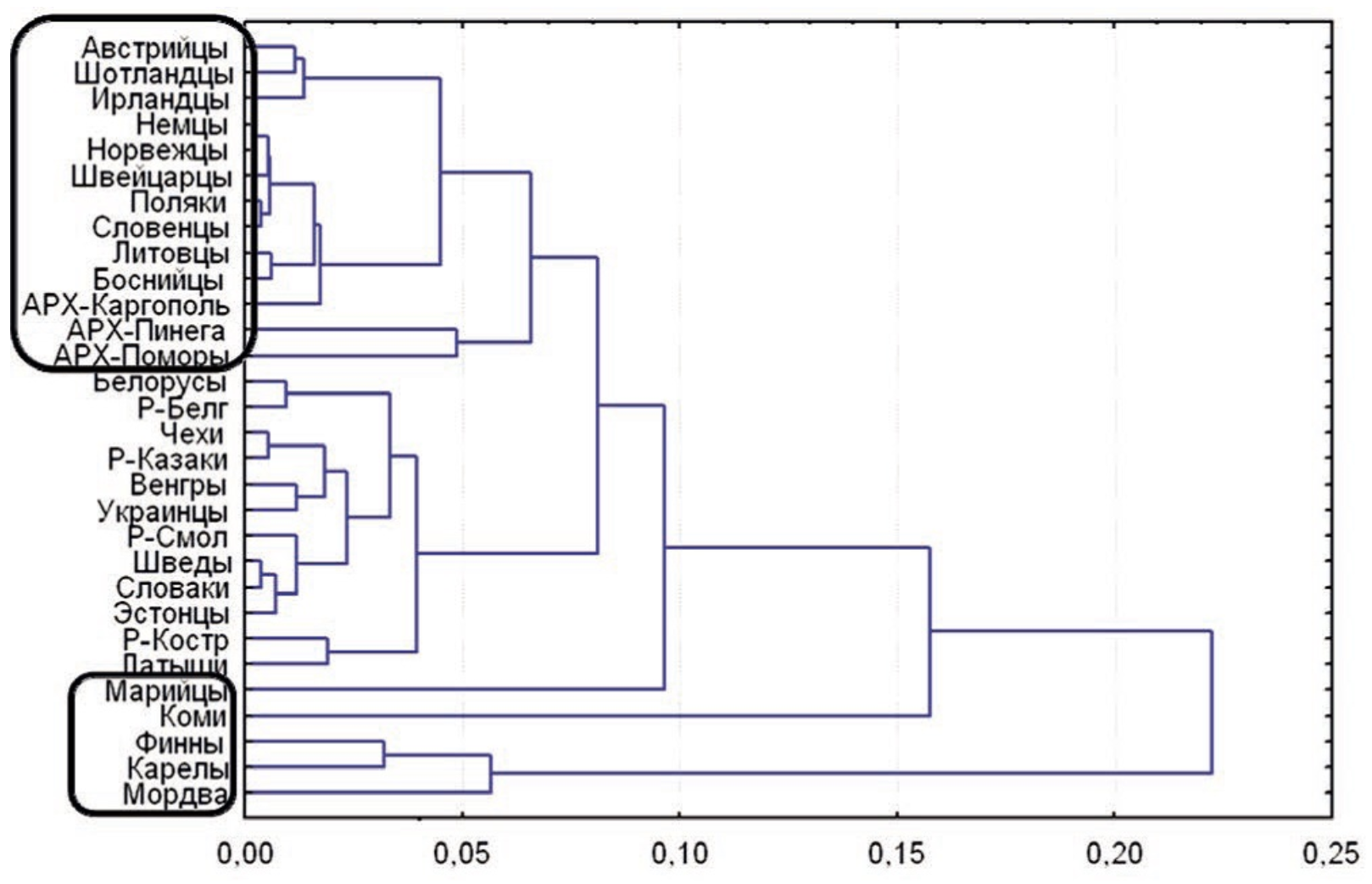
계층적 군집화는 데이터 포인트들을 점차적으로 그룹화하는 알고리즘이며, 데이터를 트리 형태의 구조로 표현한다.
덴드로그램은 계층적 군집화 결과를 시각화하는 그래프이다.
덴드로그램은 계층적 군집화에서 각 단계마다 어떤 군집이 어떤 군집과 병합되는지, 그리고 어떤 순서로 군집이 형성되었는지를 시각적으로 표현하며, 이를 통해 데이터의 군집 구조를 파악하고 최적의 군집 개수를 결정하는 데 기여한다.
군집화의 평가
1. 클러스터들 사이의 거리 최대화
클러스터 간의 거리를 최대화하여 서로 다른 클러스터들이 확실히 분리되도록 하며, 명확하게 구분되게 해야 한다.
2. 클러스터의 크기(지름) 최소화
데이터들 사이의 거리를 최소화하면, 밀집도가 높아지며, 데이터 간의 유사성이 높다고 볼 수 있다.
3. 클러스터의 분포 최소화
클러스터 내 데이터들의 분포를 최소화하여 하나의 클러스터 내에 데이터가 집중되도록 해야 한다.
분포가 적은 클러스터는 뚜렷한 특성을 가진다.
Dunn Index
클러스터링 평가 지표 중 하나로, 클러스터들 사이의 거리의 최소값을 클러스터 내의 데이터들의 분포의 최대값으로 나눈 값이다. 해당 값은 군집화의 최악의 경우를 나타낸다.
가장 가까운 다른 클러스터 데이터들 사이의 거리가 멀고, 같은 클러스터 내 데이터들이 더 밀집한 형태일수록 높은 값을 가지며 이 값이 클수록 좋다.
Silhouette
Silhouette은 각 데이터 포인트의 클러스터 내 유사성과 다른 클러스터와의 거리를 기반으로 군집화 성능을 평가한다.
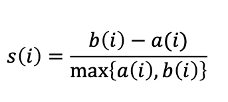
a(i) : i번째 데이터의 같은 클러스터 내의 모든 데이터로부터의 평균 거리
b(i) : i번째 데이터의 다른 클러스터 내의 데이터들 사이의 평균 거리의 최소값 -> 가장 가까운 다른 클러스터 데이터들 사이의 평균 거리
Silhouette 값은 -1에서 1 사이의 값을 가지며, 1에 가까울수록 좋은 군집화를 나타낸다.
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 비지도 학습 : 연관 규칙 분석 / 차원 축소 (0) | 2023.08.30 |
|---|---|
| [머신러닝] 비지도 학습 : K-Means Clustering (Iris dataset 군집화) (0) | 2023.08.28 |
| [머신러닝] 지도 학습 : 분류(Classification)와 모델 평가 (0) | 2023.08.28 |
| [인공지능] AI 모델의 검증 기준과 검증 방법 (1) | 2023.08.28 |
| [머신러닝] 지도 학습 : 다변량 회귀와 경사하강법 최적화 방법(Optimizer) (0) | 2023.05.03 |













