[머신러닝] 지도 학습 : 다변량 회귀와 경사하강법 최적화 방법(Optimizer)

다변량 회귀 모델
nbastat.csv(농구 점수 데이터셋)에서 야투 시도 횟수 (FGA), 3점슛 시도 횟수 (3PA), 자유투 시도 횟수 (FTA) 로부터 득점수 (PTS)를 예측하는 모델을 만들고 이를 훈련시키시오.
가설
y = 세타0 + 세타1(x1) + 세타2(x2) + 세타3(x3)
1. library import
import numpy as np
import pandas as pd
2. 드라이브 마운트 및 csv파일 업로드
from google.colab import drive
from google.colab import files
drive.mount('/lecture-2023ai')
files.upload()
nbastat = pd.read_csv('nbastat2022.csv')
m = len(nbastat)
x1 = nbastat[['FGA']] # 야투 시도 횟수
x2 = nbastat[['3PA']] # 3점슛 시도 횟수
x3 = nbastat[['FTA']] # 자유투 시도 횟수
y = nbastat[['PTS']] # 득점수
print(m, type(x1), type(x2), type(x3), type(y))
249 <class 'pandas.core.frame.DataFrame'> <class 'pandas.core.frame.DataFrame'> <class 'pandas.core.frame.DataFrame'> <class 'pandas.core.frame.DataFrame'>
4. 결측값 처리
x1 = x1.fillna(0)
x2 = x2.fillna(0)
x3 = x3.fillna(0)
y = y.fillna(0)
# Numpy로 변환
x1 = (np.array(x1)).reshape(m, 1)
x2 = (np.array(x2)).reshape(m, 1)
x3 = (np.array(x3)).reshape(m, 1)
y = (np.array(y)).reshape(m, 1)
6. 그래프로 그려보기
# 그려보기
import matplotlib.pyplot as plt
plt.plot(x1, y, '.b')
plt.plot(x2, y, '.r')
plt.plot(x3, y, '.g')
[<matplotlib.lines.Line2D at 0x7fb8f4b9ec80>]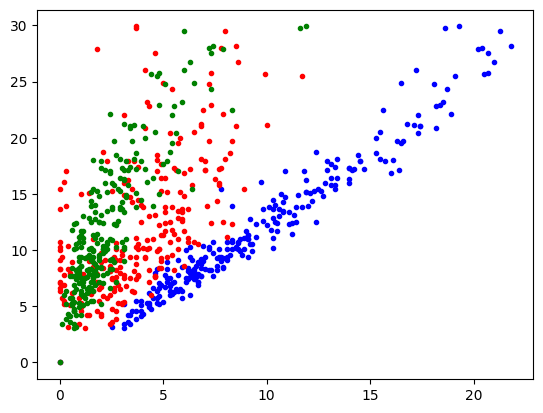
7. 경사하강을 위해 알파값과 반복임계값(iter) 설정
learning_rate = 0.0001
n_iter = 800
8. 세타값과 계산할 Gradient 초기설정, 둘 다 1x4 형태의 벡터 형태
#np.zeros((a,b)) : a * b의 Zero Matrix 생성
theta = np.zeros((4, 1)) # 세타
gradients = np.zeros((4, 1)) #Gradient
x0 = np.ones((m, 1)) #np.ones : 1로 가득 찬 array를 생성함
xb = np.c_[x0, x1, x2, x3] #np.c_ : 배열을 합침 [[1, x1, x2, x3], [1, x1, x2, x3], ...]
9. 손실 함수 정의
def j(xb, theta, y):
# 예측값 계산(현재 세타값에 대한 학습 데이터 249개의 예측값)
y_pred = np.dot(xb, theta)
# 실제값과의 차이 계산 -> 249개의 (예측값-실제값)
y_diff = y_pred - y
# 각각의 차들을 제곱 형태로 반환 -> 249개의 (차의 제곱)
#np.square : 각각의 요소를 제곱 형태로 반환
squared_diff = np.square((y_diff))
# 평균 -> 249개의 차의 제곱의 평균
#np.mean : 각각의 요소들의 평균을 반환
mean_squared = np.mean(squared_diff)
return mean_squared
10. 경사하강법을 실행하여 훈련한다.
Iterate를 반복할 때 마다 손실함수의 값을 계산하여 결과에 추가한다.
# 훈련
#np.dot(x,y) : 행렬 X와 Y의 곱
#np.T : 전치행렬
loss = []
for i in range(n_iter):
gradients = (1.0/m) * xb.T.dot(xb.dot(theta) - y)
theta = theta - learning_rate * gradients
loss.append(j(xb, theta, y))11. 결과 확인
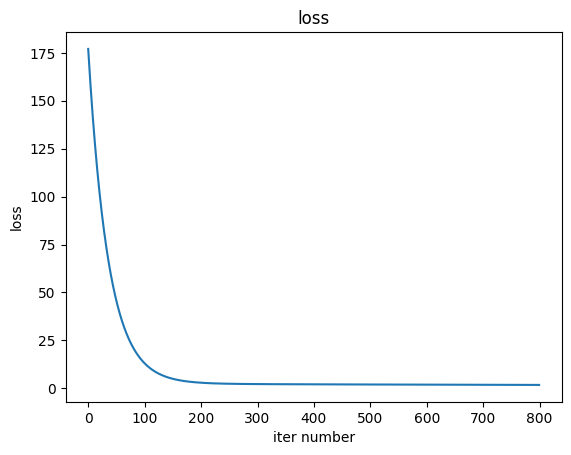
Loss 함수의 값이 수렴하는지 확인한다.
print(theta)
figure, ax = plt.subplots(1, 1) #그림과 좌표측
ax.title.set_text('loss')
ax.plot(loss)
ax.set_ylabel('loss')
ax.set_xlabel('iter number')
print('error', j(xb, theta, y))
plt.show()
xtest = np.array([1, 7, 9, 5])
result = np.dot(xtest, theta)
print(result)[[0.0850835 ]
[1.04875931]
[0.28365118]
[0.36586524]]
error 1.7613875941138313
[11.80858544]Scikit-Learn을 사용한 다항회귀
유명한 데이터셋인 diabetes에 대한 다항 회귀를 해보자
1. 라이브러리 Import
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
2. 데이터 수집
diabetes = load_diabetes()
#data와 target을 x와 y로 설정
x, y = diabetes["data"], diabetes["target"]- 라이브러리에서 제공하는 혈당 데이터를 실험용으로 사용
- 나이, 성별, BMI, 혈압 및 6개의 혈청 값과 혈당치가 저장되어 있음
- 혈당치를 예측하는 것이 목표
3. 특징 추출
- 모든 속성을 이용하기 때문에 필요없음
4. 데이터셋 분할
train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.2)
len(x), len(train_x), len(test_x), len(train_y), len(test_y)- Training Set과 Test Set으로 데이터셋을 분할
5. 모델 설계
regressor = LinearRegression()
regressor.fit(train_x, train_y) # fit은 트레이닝 함수
regressor.coef_
# 예측값
train_pred = regressor.predict(train_x)
test_pred = regressor.predict(test_x)- 라이브러리의 선형 회귀를 사용.
- fit은 라이브러리의 선형 회귀의 트레이닝 함수임
6. Loss 측정
train_mse = mean_squared_error(train_pred, train_y)
test_mse = mean_squared_error(test_pred, test_y)
print(train_mse, test_mse)- 트레이닝 셋과 테스트 셋의 Loss를 측정하여 예측값과 실측값의 차이를 측정함
Optimizer
경사 하강법을 이용한 최적화 방법
- 주식의 고점은 그때 가봐야 안다.
- 최소값을 찾기 위해서 Gradient descent를 적용하는데, J(세타)가 0이 되는 파라미터를 찾기는 힘들다.
- 따라서 경사하강의 감소폭이 특정 threshold보다 작아질 때를 최적화된것으로 간주
Learning Rate
- α(Learning Rate)에 따라 성능이 결정됨
- 너무 작은 α는 학습 진행속도가 느리다.
- 너무 큰 α는 학습이 진행이 되지 않는다.
Gradient Descent의 문제점
- 시간 : 학습 데이터가 너무 많은 경우 시간이 오래 걸림
- SGD : 확률적 경사하강법. 학습 데이터 전체를 사용하지 않고 Batch Size만큼 학습하며 업데이트 -> 학습 속도를 높이고 메모리 사용량을 줄일 수 있음
- Local Minimum : Global Minimum을 찾아야 하는데 Local Minimum에 수렴하여 멈출 수 있음.
- Momentum : Local Minumum 문제를 극복하기 위해서 관성 적용. 이전 기울기 방향과 같은 방향이라면 속도를 가속한다.
- NAG : Momentum과 비슷하지만 예상을 먼저 진행한다. (먼저 관성에 따라서 갈 곳의 기울기값을 판단 → 실제로 이동)
- Gradient Vanishing : 기울기가 점점 작아져 0에 가까워지는 현상. 딥러닝에서는 초기 Layer의 가중치가 거의 업데이트되지 않아 학습이 어려워지는 문제가 발생할 수 있다.
- Gradient Exploding : 기울기가 너무 커져서 수렴하지 못하는 현상. 딥러닝에서는 가중치가 급격하게 변동하는 현상이 발생하여 불안정을 초래한다.
- 각 변수별 Gradient의 크기가 다름 : 학습 속도 차이 -> 특정 변수의 수렴이 이루어지지 않을 수 있음
- AdaGrad : 각 단계, 각 파라미터 마다 학습률을 다르게 적용
- 드물게 등장하는 변수에 대해서 Step size를 크게 해줌
- 자주 등장하는 변수에 대해서 Step size를 작게 해줌 -> 그렇지만 학습률이 너무 적어져 Gradient Vanishing이 발생할 수 있음
- RMSProp : AdaGrad의 학습률 감소 문제 해결 → 최근 그래디언트만을 고려하여 학습률을 조정
- Adam : AdaGrad와 RMSProp을 결합한 방식.
Gradient Descent 문제의 해결 방법
1. Momentum
- 이전에 계산된 기울기를 이용하여 현재 기울기의 방향과 크기를 결정하는 방법
- 즉 해당 시점에서의 과거의 이동 거리의 평균을 내서 같이 고려하는 방법
- SMA(단순 이동 평균) : 과거 i개를 보고 평균을 낸다. 그러나 비교적 가까운 과거와 먼 과거를 고려하지 않음
- LWMA(가중 이동 평균) : 가까운 시기의 데이터에 더 높은 가중치를 부여함
- EMA(지수 이동 평균) : 가중치가 지수 분포를 따르게 한다. 멀리 있을수록 지수를 곱해서 Weight를 떨어뜨린다. 그래디언트에 이 가중치를 모두 더한 값을 함께 사용함. 기울기가 0이 되더라도 모든 지난 Gradient 가중치를 더해서 0이 아니면 v(t)에 의해 추진력을 받아 계속 이동하게 함
2. AdaGradient
- 변수별로 그래디언트가 다를 수 있다 -> 특정 변수 수렴안됨
- Gradient의 누적값을 계산해서 분모에 넣고 계산하면 클 수록 많이 줄어들 것이다.
- 그러나 누적값이 매우 커질 경우 값이 아주 작아지게 되어 학습이 이루어지지 않음
3. RMSProp
- AdaGradient의 문제 보완
- Gradient의 누적값 계산에 지수이동평균(EMA)을 도입한다.
4. ADAM
- Momentum과 AdaGradient를 함께 적용하여 계산하는 방식
- Gradient을 지수 이동 평균 누적값으로 나눈 값들에 Momentum을 적용시킨다.
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 비지도 학습 : 군집화(Clustering) (0) | 2023.08.28 |
|---|---|
| [머신러닝] 지도 학습 : 분류(Classification)와 모델 평가 (0) | 2023.08.28 |
| [인공지능] AI 모델의 검증 기준과 검증 방법 (1) | 2023.08.28 |
| [인공지능] AI 개요와 라이프사이클 (0) | 2023.05.03 |
| [머신러닝] - 지도 학습 : 방법론과 단순 선형 회귀 구현 (0) | 2023.03.25 |













