[머신러닝] - 지도 학습 : 방법론과 단순 선형 회귀 구현

AI = Model + Data
Model : y = Ax + B (선형 회귀 모델)
- Model = Code(식) + Parameter(A, B)
Data: [(x1, y1), (x2, y2), (x3, y3)...]
1. 수집된 데이터와 목적에 따라서 모델을 결정하고
2. 데이터를 통해 학습시키며 최적의 모델의 파라미터를 구하는 것이 우리가 할 일
3. AI와 데이터는 닭과 계란의 관계
- AI -> 데이터 : 우수한 분석 도구
- 데이터 -> AI : AI 모델 훈련에 필요
데이터의 종류
정형 데이터 : 속성을 명확하게 정의할 수 있는 데이터
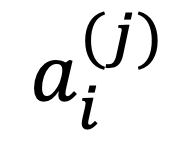
- 데이터 하나는 다음과 같이 표현
- i : 속성의 인덱스 (0 <= i <= n - 1)
- j : 개체의 인덱스 (0 <= j <= m - 1)
- 키, 몸무게, 나이를 가진 21명의 사람들 -> n = 3, m = 21
비정형 데이터 : 속성을 명확하게 정의할 수 없는 데이터 (영상, 음성, 문장)
하이브리드 데이터: 두 가지 성질을 모두 가짐 (사진 + exif 정보)
데이터 수집
크롤링, 오픈 데이터셋 활용, 데이터 구매, 제공 API 활용, 직접 수집 등..
데이터 정제와 특징 추출
1. 목적과 상관없는 속성 제거
2. 이상 원소 제거
- 미국 UNC 학과 중 졸업생 연봉이 가장 높은 학과를 알아내려고 할 때, 지리학과가 가장 높게 나온다. 마이클 조던이 비정상적으로 연봉이 높기 때문
3. 특징 추출
- 목적 의사판단에 결정적인 속성을 추려내는 과정
- 선수가 필드 슛을 시도할 때 몇 개의 슛을 성공하는지를 예측할 때 관심있는 속성은 필드 슛(FGA), 성공 슛(FGM)이다.
- Explict feature : 명확하게 숫자로 나오는 특징
- Implict feature : 두 사진을 같은 사람으로 판단할 수 있는 근거?(특징) : 비정형 데이터에 해당하는 경우가 많음
ML Model 설정
1. 지도 학습 vs 비지도 학습
| 지도 학습 |
비지도 학습 | |
| Label이 있는 데이터, 데이터에 대해서 Label을 예측하도록 훈련 | Label이 없는 데이터, 데이터에서 특징을 추출하여 집단을 찾도록 훈련 | |
| 범주형 변수 | 연속형 변수 | 추상화된 그룹으로 나눔 |
| 분류 | 회귀 | 군집화 |
2. 지도 학습 모델의 종류
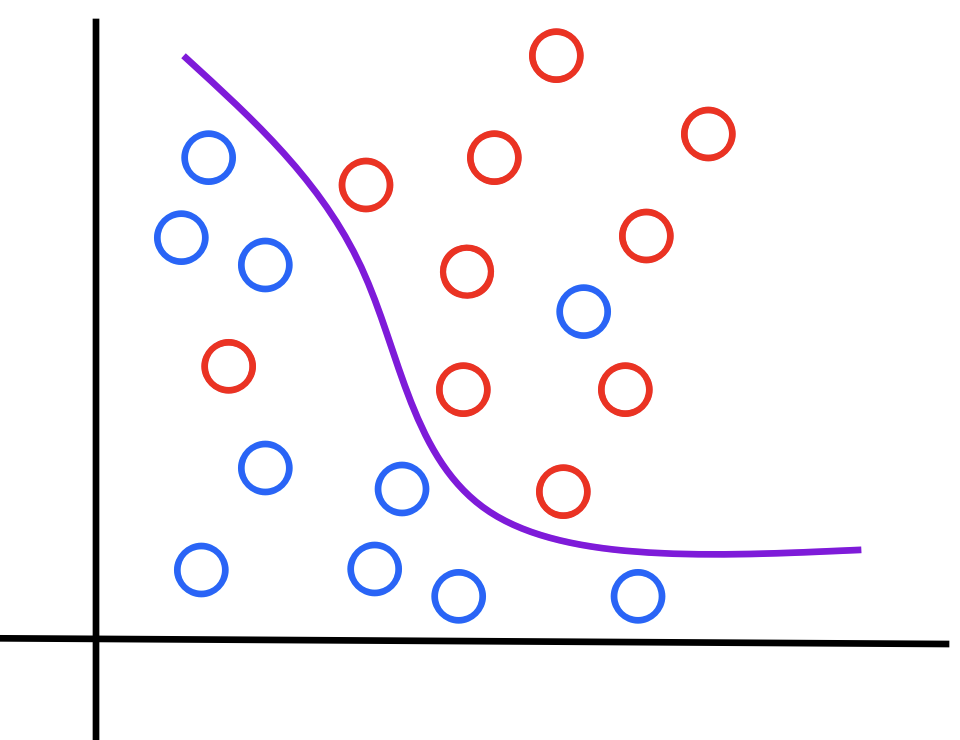
2-1. 분류, 인식 (Classification / Recognition)
- 범주형 변수를 예측하는 모델
- 입력된 데이터가 어떤 클래스(레이블)에 속하는지를 판정
- 학습 데이터는 레이블된 데이터를 사용
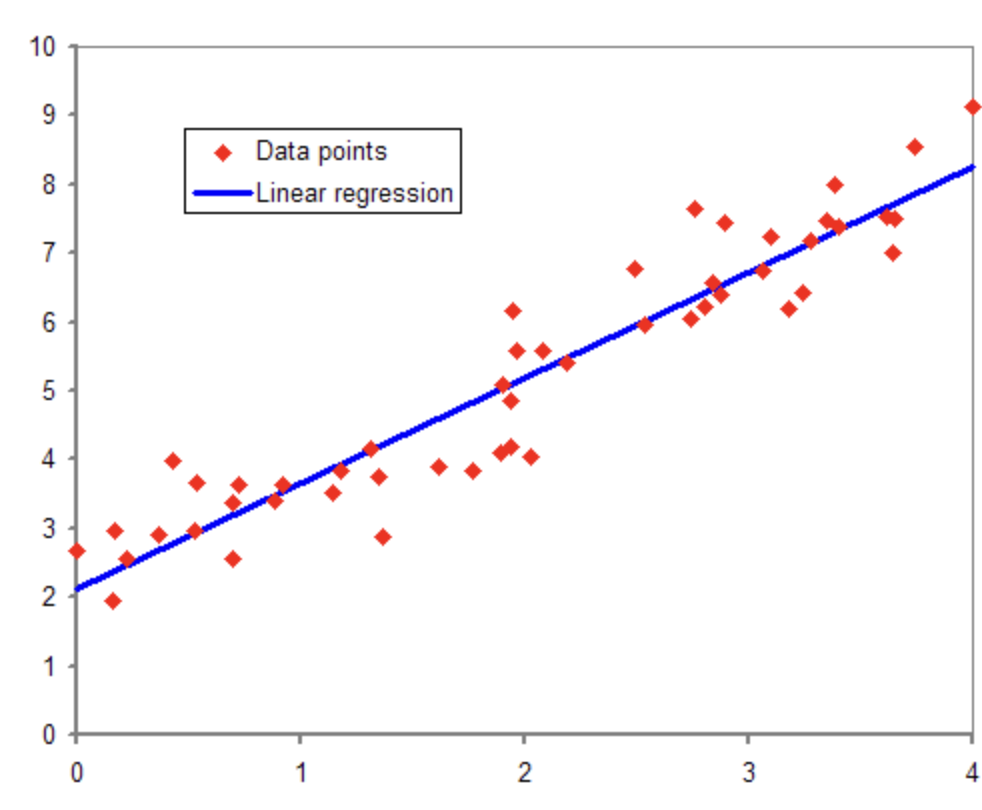
2-2. 회귀 (Regression)
- 연속형 변수를 예측하는 모델
- 입력된 데이터로부터 특정한 값을 예측
3. 비지도 학습 모델의 종류
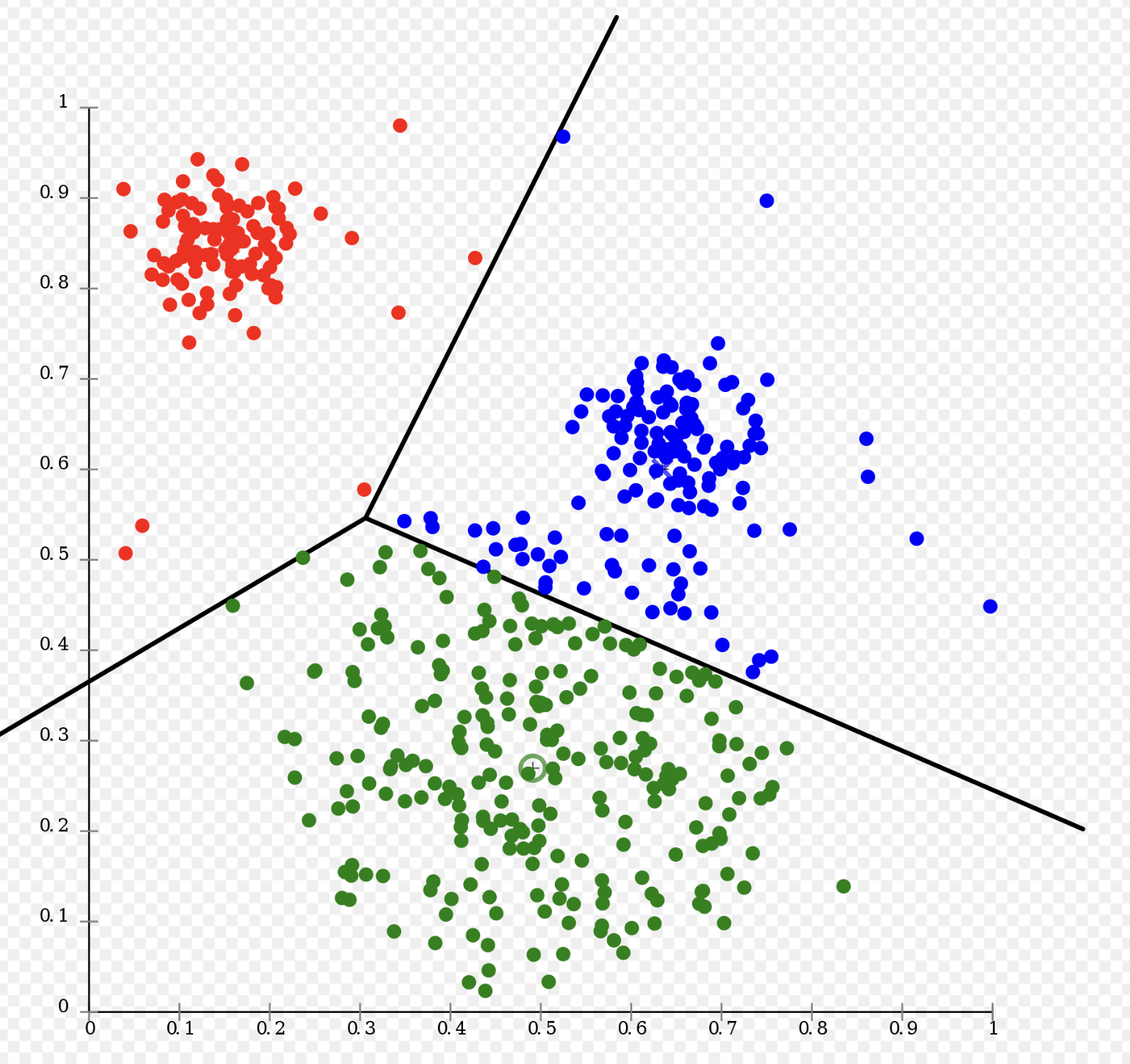
3-1. 군집화 (Clustering)
- 범주형 변수를 예측하는 모델
- 입력된 데이터의 특징을 추출하여 유사한 집단을 파악
- 레이블이 없는 데이터로 학습하므로, 명확한 카테고리가 결정되는 것이 아니라 유사 집단으로 묶는 것
- 즉 분류 모델과 달리 지정된 클래스로 할당하는 것이 아님
4. ML 모델의 설정
4-1. 입력 속성의 개수 : 단변량(단수), 다변량(복수)
4-2. Model의 종류(Output) : 분류 vs 회귀 vs 군집화 vs ???
4-3. Model의 복잡도 : 선형 < 다항 < Logistic < ???
ML 모델의 훈련
모델을 준비한 후 모델의 최적 파라미터를 구하기 위해서 훈련
1. 문제 설정과 데이터 준비
NBA에서 어떤 선수가 필드 슛(FGA)를 시도할 때, 몇개의 슛을 성공(FGM)하는지를 예측
2022년도의 미국 프로 농구의 선수 데이터를 활용 (nbastat2022.csv)
2. 모델 훈련 준비와 데이터 그려보기
import numpy as np
import pandas as pd
from google.colab import drive
drive.mount('/lecture-2023ai')
from google.colab import files
# files.upload()
nbastat = pd.read_csv('nbastat2022.csv')
m = len(nbastat)
x = nbastat[['FGA']] # 필드 슛 시도
y = nbastat[['FGM']] # 슛 성공 개수
# 결측값 처리
x = x.fillna(0)
y = y.fillna(0)
# Numpy로 변환
x = (np.array(x)).reshape(m, 1)
y = (np.array(y)).reshape(m, 1)
# 그려보기
import matplotlib.pyplot as plt
plt.plot(x, y, '.b')
plt.xlabel('FGA')
plt.ylabel('FGM')
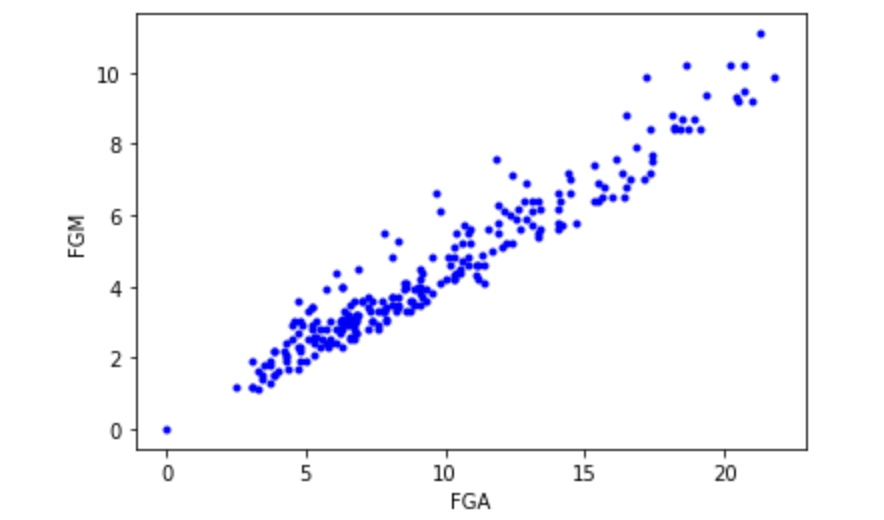
데이터를 훈련시킬 준비를 거친다. 데이터를 그려보니 y = Ax + B 형태의 선형 회귀 모델을 이용해서 훈련하려고 함
우리가 해야할 일은 A와 B를 결정하는 것 (θ(0)과 θ(1)로 표현)
3. 손실 함수와 경사 하강법
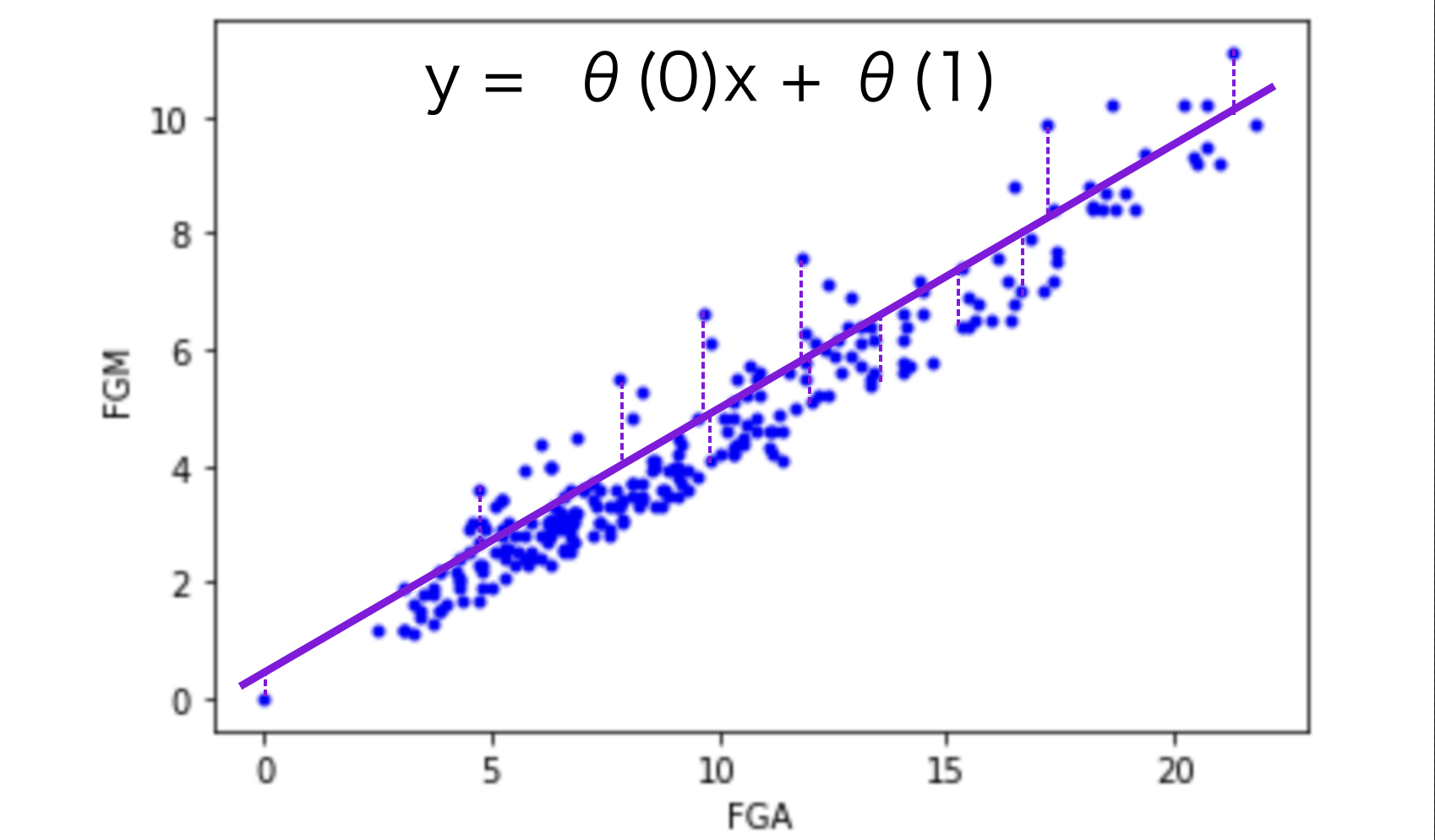
다음과 같이 선형 회귀 모델의 최적 파라미터를 구하기 위해서는 임의의 θ(0)과 θ(1)을 설정하여 가설 함수를 만들 수 있다.
보라색 점선과 같이 각각의 데이터들은 가설 함수와의 차이가 나게 되며, 해당 차이가 최소화되는 θ(0)과 θ(1)이 최적 파라미터라고 할 수 있으며, 손실이 덜하다고 볼 수 있다. 해당 차이를 바탕으로 무수한 가설 함수들에 대해서 아래의 손실 함수를 작성할 수 있다.
손실 함수
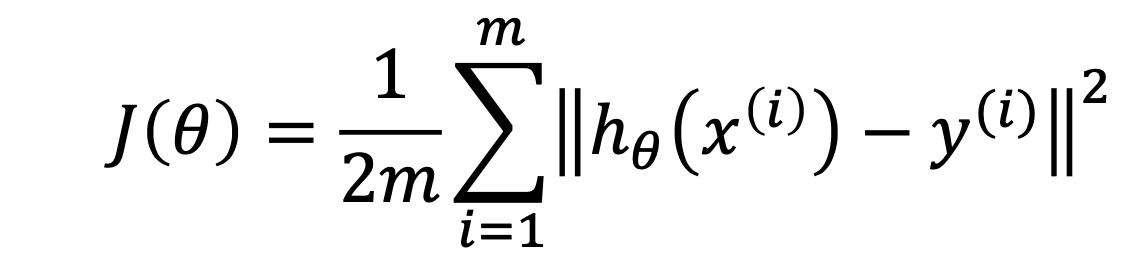
각각의 가설 함수에 대해서의 손실의 정도를 나타내는 함수이다.
m개의 모든 데이터에 대해서 (가설 함수의 i번째 데이터의 예측값 - i번째 원래 데이터 값)의 제곱을 구한 후 평균을 구하는 MSE(Mean Squared Error, 평균제곱오차)를 정의하여 손실 함수를 만든다.
평균을 구할 때 분모에 2를 곱한 것은 계산의 편의상이다.
선형 회귀 함수에서의 손실 함수는 다음과 같이 표현된다.

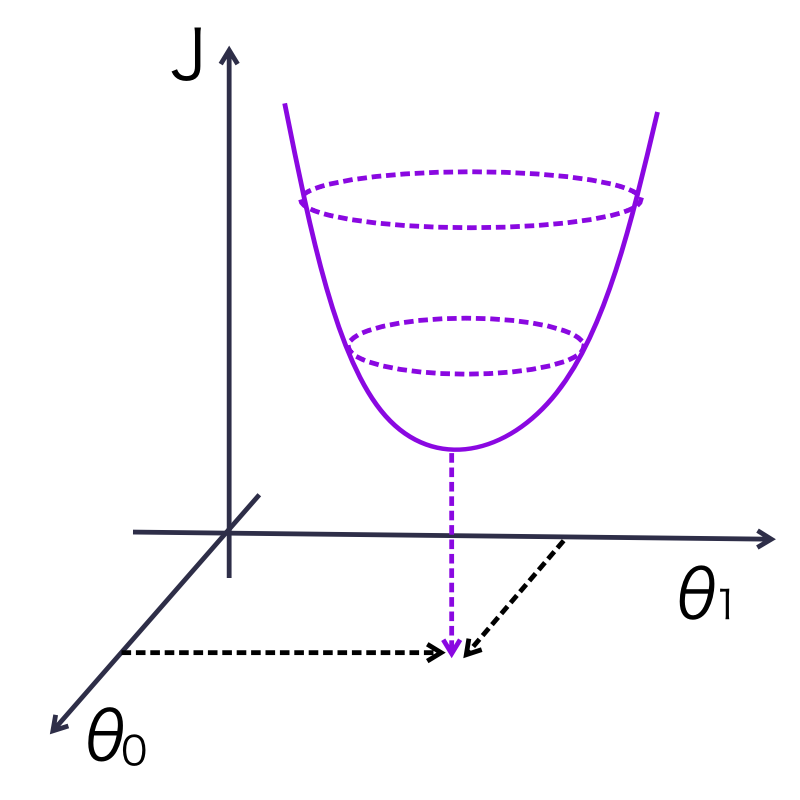
경사 하강법
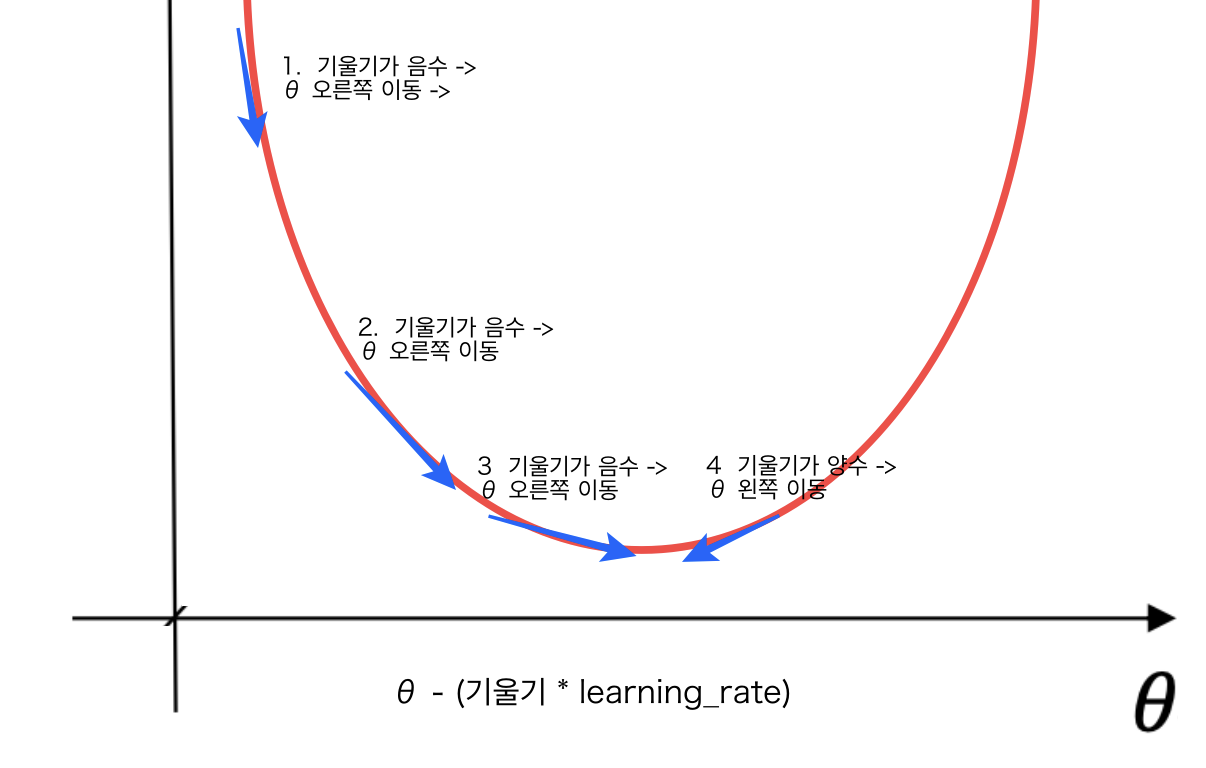
- 경사 하강법은 머신러닝 모델의 옵티마이저(최적화 도구)의 종류이다.
- 손실 함수의 값이 최소화되도록 모델 파라미터를 조정한다.
- 위의 그림과 같은 손실 함수가 있다고 치자, 어떤 점에서의 미분계수가 음수면 오른쪽으로, 미분계수가 양수면 왼쪽으로 이동해야 최소값을 구할 수 있다.
- θ - (미분 계수 * learning_rate)의 과정을 반복하며 세타를 이동시키면서 손실 함수의 최소값을 찾게 된다.
- 최소 값을 구하기 위해서 θ를 어느 방향으로, 얼마만큼 이동시킬지를 결정해야 하며, 미분계수가 그 역할을 한다.
- 미분계수의 부호에 따라서 방향을, 또한 최소값에 근접할 수록 미분계수가 작아지므로, 최소값에서 멀 때는 빠르게 수렴하고, 가까울 때에는 천천히 수렴하게 할 수 있다.
- Learning rate는 모델의 학습률 파라미터이며, 이동하는 거리를 조절하는 데에 역할을 한다.

- 따라서 다음의 손실 함수의 최소값을 구하기 위해서 미분계수를 구해야 하는데, 두 개의 변수에 대해서 미분해주어야 한다.
- 3차원 상에서 손실함수의 최소값에 가장 근접하는 (θ(0),θ(1))의 좌표를 구하는 것이 목표
Gradient 계산
 |
 |
- 기울기를 구하는 식을 벡터식으로 표현하면 다음과 같다. θ(0), θ(1)에 대해서 각각 편미분하면 기울기 도출 식이 나온다.
- 결과는 (θ(0)의 편미분, θ(1)의 편미분)의 1x2의 벡터가 나올 것이다.
4. 훈련
import numpy as np
import pandas as pd
from google.colab import drive
drive.mount('/lecture-2023ai')
from google.colab import files
files.upload()
nbastat = pd.read_csv('nbastat2022.csv')
m = len(nbastat)
x = nbastat[['FGA']] # 필드 슛 시도
y = nbastat[['FGM']] # 슛 성공 개수
# 결측값 처리
x = x.fillna(0)
y = y.fillna(0)
# Numpy로 변환
x = (np.array(x)).reshape(m, 1)
y = (np.array(y)).reshape(m, 1)
learning_rate = 0.0001 # Learning Rate
n_iter = 949 # 반복 횟수
#np.zeros((a,b)) : a * b의 Zero Matrix 생성
theta = np.zeros((2, 1)) # 세타
gradients = np.zeros((2, 1)) #손실값
x0 = np.ones((m, 1)) #np.ones : 1로 가득 찬 array를 생성함
xb = np.c_[x0, x] #np.c_ : 배열을 합침 [[1, x1], [1, x2], ...]
# 훈련
#np.dot(x,y) : 행렬 X와 Y의 곱
#np.T : 전치행렬
for i in range(n_iter):
# Gradient 도출식
gradients = (1.0/m) * xb.T.dot(xb.dot(theta) - y)
# 현재 기울기에 비례하여 세타(0),세타(1) 경사하강법으로 이동
theta = theta - learning_rate * gradients
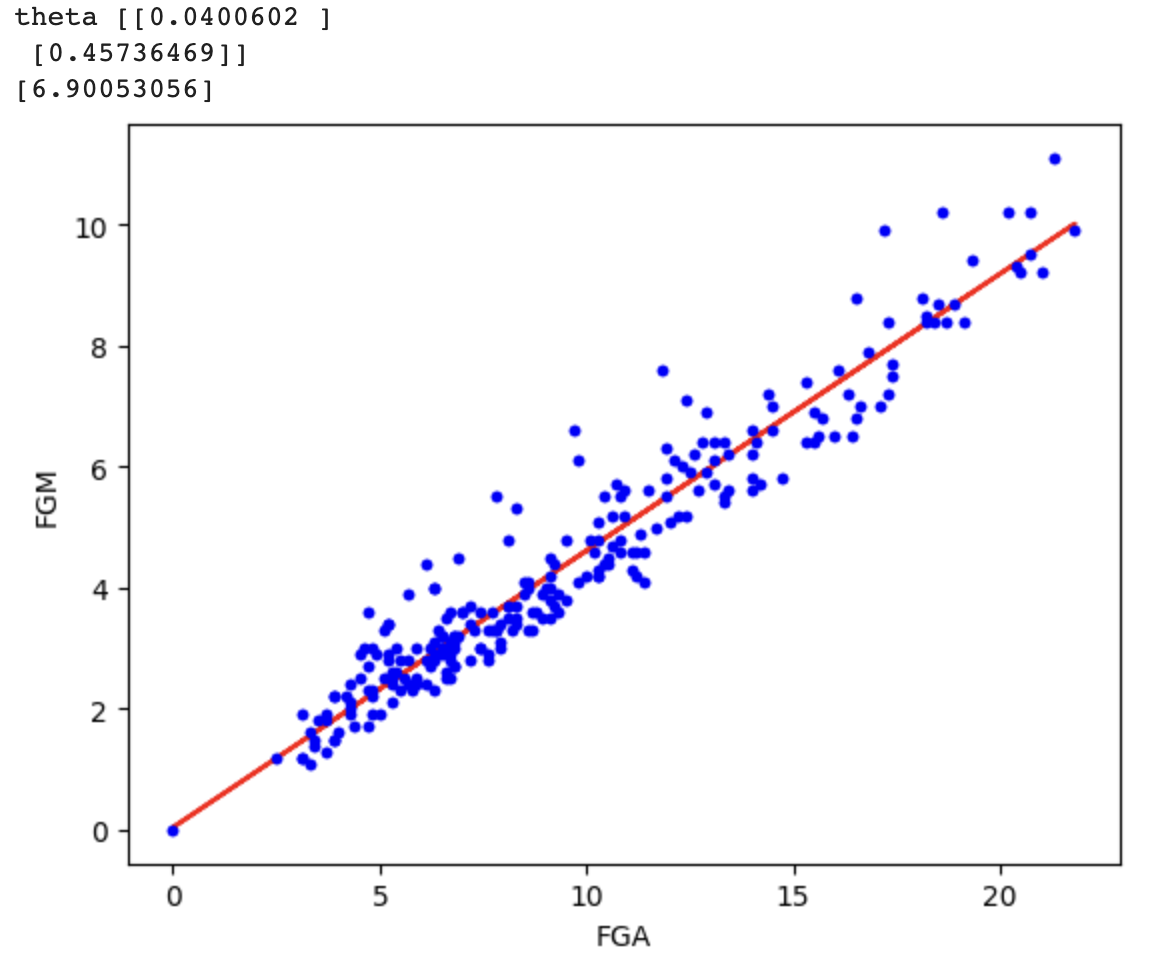
print('theta', theta)
# 결과
y_pred = xb.dot(theta)
plt.plot(x, y_pred, color='Red')
plt.plot(x, y, '.b')
xtest = np.array([1, 15])
result = np.dot(xtest, theta)
print(result)
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 비지도 학습 : 군집화(Clustering) (0) | 2023.08.28 |
|---|---|
| [머신러닝] 지도 학습 : 분류(Classification)와 모델 평가 (0) | 2023.08.28 |
| [인공지능] AI 모델의 검증 기준과 검증 방법 (1) | 2023.08.28 |
| [머신러닝] 지도 학습 : 다변량 회귀와 경사하강법 최적화 방법(Optimizer) (0) | 2023.05.03 |
| [인공지능] AI 개요와 라이프사이클 (0) | 2023.05.03 |












