[머신러닝] 비지도 학습 : 연관 규칙 분석 / 차원 축소

포스팅된 글의 인용한 모든 이미지는 CCL 라이선스의 이미지만을 사용했으며, 출처를 밝힙니다.
비지도 학습
- Label이 없는 데이터를 학습시키는 방법
- 유사성을 기반으로 그룹화하거나 데이터에 숨어있는 구조를 파악
비지도 학습의 종류
- 군집화 : 데이터로부터 몇 개의 대표적인 집합을 얻어내는 방법
- 연관 규칙 분석 : 항목들 사이의 관계를 분석하여 연관성을 찾는 방법
- 차원 축소 : 높은 차원의 데이터를 낮은 차원의 데이터로 변환하는 방법
연관 규칙 분석
연관 규칙 분석은 비지도 학습의 한 종류로서, 데이터에서 아이템 간의 연관성을 찾아내는 기법.
이를 통해 데이터 집합 내에서 아이템들 간의 패턴, 규칙, 관계를 발견하거나 예측하는 데 사용된다.
연관 규칙 분석의 대표적인 예는 슈퍼마켓에서의 장바구니 분석이며, 예를 들어, 소비자들이 어떤 제품들을 함께 구매하는지를 조사하여 "만약 A를 샀다면 B도 살 확률이 높다"라는 규칙을 찾아낸다.
아래는 연관 관계 분석에서 사용되는 지표들이다.
A가 발생할 때 B가 함께 발생한다는 규칙에 대한 예시를 통해 지표를 설명하였다.
- 지지도 (Support):
특정한 규칙이 데이터에서 얼마나 빈번하게 나타나는지를 나타내는 지표. A와 B가 함께 나타나는 빈도를 측정
P(A n B) - 신뢰도 (Confidence):
A가 발생할 때 B가 발생할 조건부 확률, 어느 정도로 신뢰할 수 있는지를 측정
지지도가 작으면 신뢰도가 의미가 없음
P(B|A) = P(A n B) / P(A) - 향상도 (Lift):
A와 B가 독립적으로 발생할 확률(독립시행)에 비해 동시에 발생할 확률이 얼마나 높은지를 보여주는 지표.
A의 추가가 B의 발생을 얼마나 향상시키는 지 측정
향상도 > 1 : 상호이익 / 향상도 = 1 : 독립적관계 / 향상도 < 1 : 상호반대
P(B | A) / P(B) - 레버리지 (Leverage):
A와 B의 동시 발생 횟수를 독립사건 횟수와 비교하여 측정한 값
레버리지>0 : 상호이익, 레버리지=0 : 독립적관계, 레버리지<1: 상호반대
P(A n B) / P(A) * P(B) - 확신도 (Conviction):
A가 주어졌을 때 B가 발생하는데 독립사건 확률에 비해 얼마나 더 자주 발생하는지를 측정
(1 - P(B)) / 1 - (P(B | A))
차원 축소
비지도 학습의 종류
차원 = 데이터 속성의 수, 지나치게 많은 데이터의 속성을 줄임
차원 축소는 고차원 데이터를 저차원 공간으로 변환하는 기법을 의미하며, 이를 통해 데이터의 특징을 보존하면서 데이터의 복잡도를 줄인다. 차원 축소의 주요 목적은 데이터의 특성을 요약하거나 시각화를 용이하게 하여 데이터 처리와 분석을 효율적으로 하도록 돕는다.
PCA
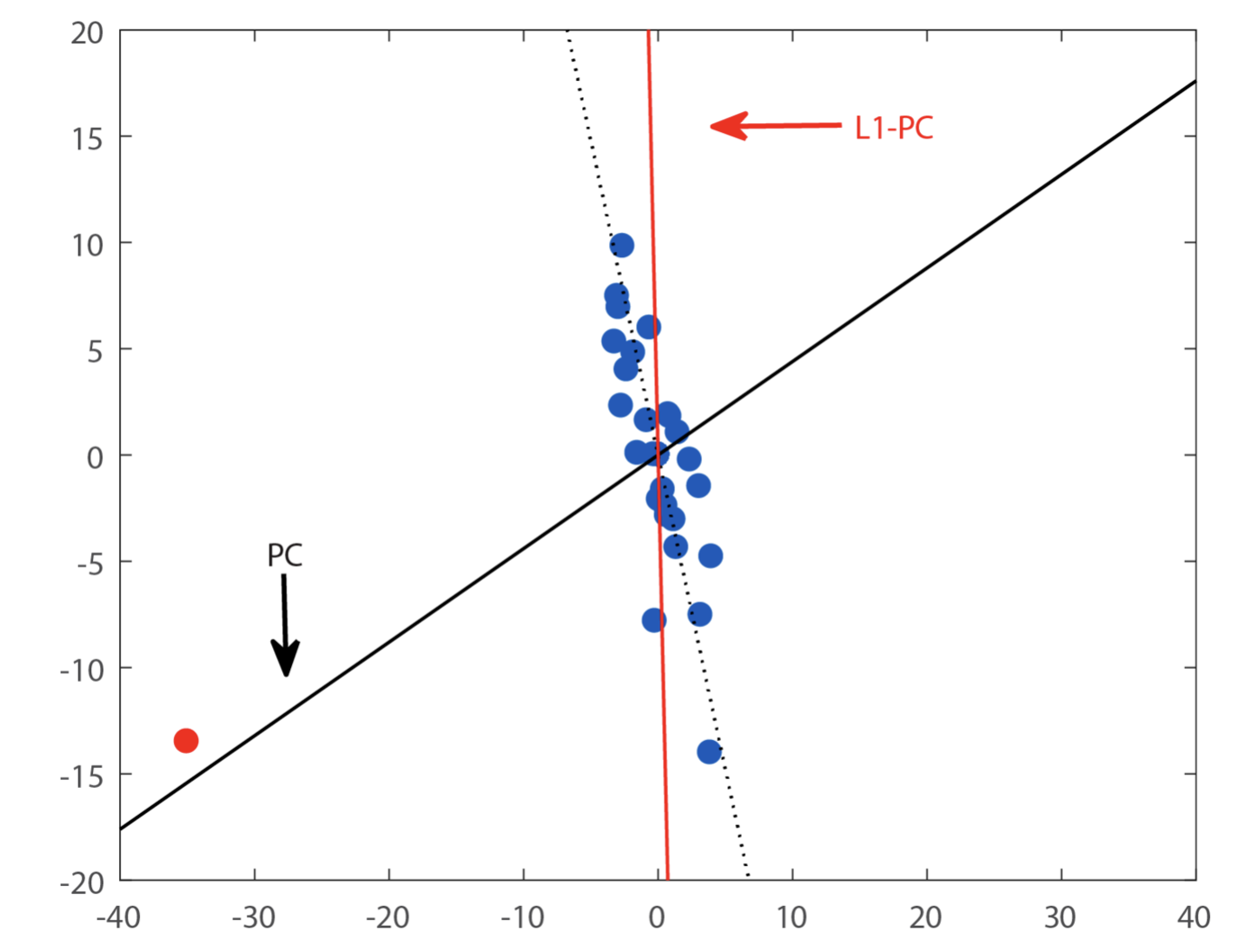
PCA는 데이터의 주요 정보를 보존하면서 차원을 축소할 수 있다. 데이터 시각화, 노이즈 제거, 데이터 압축, 분류 등에서 사용된다.
PCA는 속성 간의 상관관계를 이용하여 데이터의 속성을 줄이고, 원본 데이터의 분산을 최대한 보존하는 새로운 좌표축을 찾아내어 데이터를 임의의 축으로 Projection 한다. 이러한 새로운 좌표축은 주성분이라고 부르며, 데이터의 분산이 큰 순서대로 정렬된다.
분산을 Maximize 하는 것이 가장 큰 목표이다.
데이터 정규화: 차원 축소를 수행하기 전에 데이터를 평균 0, 분산 1로 정규화
공분산 행렬 계산: 정규화된 데이터의 공분산 행렬을 계산 이 행렬은 데이터 간의 상관관계를 나타내며, 주성분을 찾는 데 활용
고유값 분해: 공분산 행렬을 분해하여 주성분과 고유값을 구한다. 고유값은 주성분의 중요도를 나타내며, 이 값이 큰 순서대로 주성분을 선택
주성분 선택: 고유값이 큰 주성분을 선택하여 새로운 좌표축으로 사용
새로운 좌표 계산: 선택한 주성분을 기반으로 원본 데이터를 새로운 좌표계로 투영
'Data Science > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝] 앙상블 모델 : Boosting / Stacking 적용해보기 (0) | 2023.08.30 |
|---|---|
| [머신러닝] 앙상블 모델 : Voting / Bagging / Random Forest 적용해보기 (0) | 2023.08.30 |
| [머신러닝] 비지도 학습 : K-Means Clustering (Iris dataset 군집화) (0) | 2023.08.28 |
| [머신러닝] 비지도 학습 : 군집화(Clustering) (0) | 2023.08.28 |
| [머신러닝] 지도 학습 : 분류(Classification)와 모델 평가 (0) | 2023.08.28 |













