[알고리즘/JAVA] 그래프 위상 정렬 (Topological Sort)

위상 정렬(Topological Sort)
사이클이 없는 그래프에서 노드의 순서를 찾는 알고리즘
그래프 내의 노드들 간의 선후 관계를 결정하여, 어떤 작업들이 먼저 수행되어야 하는지 순서를 정하는 것이 목표이다.
작업의 선후 관계를 결정해야 하거나 특정 순서로 작업을 처리해야 하는 문제에서 사용된다.
특징
- 위상 정렬은 방향 그래프에서 사용된다. 노드들 간의 방향성이 있는 의존 관계를 표현하기 위해서 위상 정렬을 수행하는 것이기 때문이다.
- 그래프에 사이클이 없어야 한다. 사이클이 존재하면 위상 정렬이 불가능하다.
- 이 점을 이용하여 반대로 위상 정렬을 수행하여 사이클을 탐지할 수 있다.
- 위상 정렬 결과는 항상 유일하지는 않다. 즉 동일한 그래프에 대해 여러 가지 정렬 결과가 나올 수 있다.
- 시간 복잡도는 O(V+E), (V는 그래프의 노드 수, E는 간선 수)
위상 정렬 수행 과정
1. 그래프 데이터 → 그래프 구현(인접 행렬 or 리스트) + 진입차수 배열 D 초기화

위상 정렬은 진입 차수 배열에 의해서 이루어진다. 그래프를 만들면서 각 노드 별 진입차수를 계산하여 배열을 초기화시켜준다.
이 때 진입차수가 0인 배열은 선행되어야 하는 조건(노드)가 없다는 뜻이다. 따라서 가장 우선적으로 수행되어야 하는 작업(우선적으로 정렬되어야 하는 노드)라는 뜻이다.
2. 맨 처음 진입 차수가 0인 노드를 선택하여 큐에 저장
선입선출 구조로 순차적으로 위상 정렬을 하기 위해서 큐를 사용한다. 큐에 들어오는 노드는 진입 차수가 0인 노드들이며, 이를 Polling하면서 정렬과 동시에 다른 노드들을 업데이트 한다.
3. 큐에서 노드를 꺼내어 선택한 노드가 가리키는 노드들의 D(진입 차수 배열)를 1씩 감소 + 정렬 결과에 추가

큐에서 선택한 노드를 처리하는 과정이다. 해당 노드들은 진입차수가 0인, 즉 선행조건이 존재하지 않거나 앞 단계에서 처리가 완료되어 현재 정렬 우선순위가 가장 높은 노드들이다.
해당 노드들을 노드들을 정렬 결과에 추가하면서 동시에 인접 리스트로 이어져있는 하위 노드들의 진입 차수를 1씩 감소시켜준다.
이것은 하위 노드들 입장에서는 선행 조건중 하나가 처리가 완료되었다는 것을 의미하며 이것을 갱신해주는 과정이다.
만약 하위 노드의 진입 차수가 0이 된다면 큐에 추가해준다.
4. 모든 노드의 방문이 완료되어 진입 차수 배열이 모두 0이 될 때 까지 반복
모든 노드를 처리하고, 진입 차수 배열 D의 모든 값이 0이 되면 위상 정렬이 성공적으로 완료된 것이다.
위상 정렬을 성공적으로 완료하면 그래프는 사이클이 없는 DAG임을 의미한다.
위상 정렬이 중간에 멈추거나 큐가 비어도 모든 노드를 방문하지 못했다면 이는 그래프에 사이클이 존재함을 의미한다.
문제 : 위상 정렬 구현 (백준 2252, 줄 세우기)
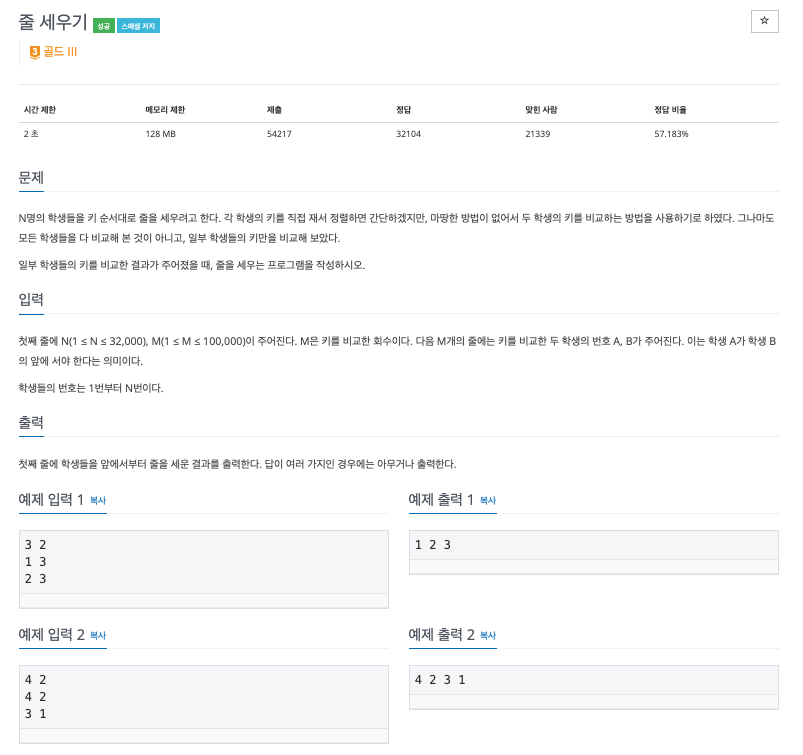
요소들의 선후 관계 파악 + 방향 그래프로 표현 가능한 문제는 위상 정렬을 사용하면 해결할 수 있는 문제이다.
위에서 살펴보았던 위상 정렬의 과정을 충실하게 구현하면 된다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 노드의 수 (정점 수)
int m = Integer.parseInt(st.nextToken()); // 간선의 수
int[] D = new int[n+1]; // 진입 차수 배열, 각 노드의 진입 차수를 기록
List<Integer>[] graph = new LinkedList[n+1]; // 그래프를 인접 리스트로 표현
// 그래프 초기화
for(int i = 1; i <= n; i++){
graph[i] = new LinkedList<>();
}
// 그래프의 간선 정보를 입력받고, 진입 차수를 계산
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
graph[a].add(b); // 노드 a에서 노드 b로의 간선을 추가
D[b]++; // 노드 b의 진입 차수를 증가
}
Queue<Integer> queue = new LinkedList<>(); // 진입 차수가 0인 노드를 담을 큐
for(int i = 1; i <= n; i++){
if(D[i] == 0){ // 진입 차수가 0인 노드를 찾음
queue.offer(i); // 큐에 추가
}
}
StringBuilder sb = new StringBuilder(); // 결과 출력을 위한 StringBuilder
while(!queue.isEmpty()){
int current = queue.poll(); // 큐에서 노드를 꺼내 처리
sb.append(current).append(" "); // 해당 노드를 결과에 추가 (위상 정렬 결과)
for(int next : graph[current]){ // 현재 노드에 연결된 노드들에 대해
D[next]--; // 연결된 노드들의 진입 차수를 감소
if(D[next] == 0){ // 진입 차수가 0이 되면
queue.offer(next); // 큐에 추가
}
}
}
System.out.println(sb); // 위상 정렬 결과 출력
}
}
진입 차수 배열(D): 각 노드로 들어오는 간선의 수를 기록하고 진입 차수가 0인 노드를 찾기 위해 사용한다.
큐: 현재 우선순위가 가장 높은(처리되어야 하는 노드, 진입 차수가 0인 노드)를 선입선출로 처리한다.
그래프 인접 리스트: 노드 간의 연결 관계를 그래프로 표현하여 위상 정렬을 수행할 때 노드 간의 의존성을 관리한다.
위상 정렬 과정
- 진입 차수가 0인 노드를 먼저 처리
- 해당 노드와 연결된 다른 노드들의 진입 차수를 갱신
- 연결된 노드의 진입 차수가 0이 되면 큐에 추가
문제 : 위상 정렬의 특징 유의하기 (백준 3665, 최종 순위)
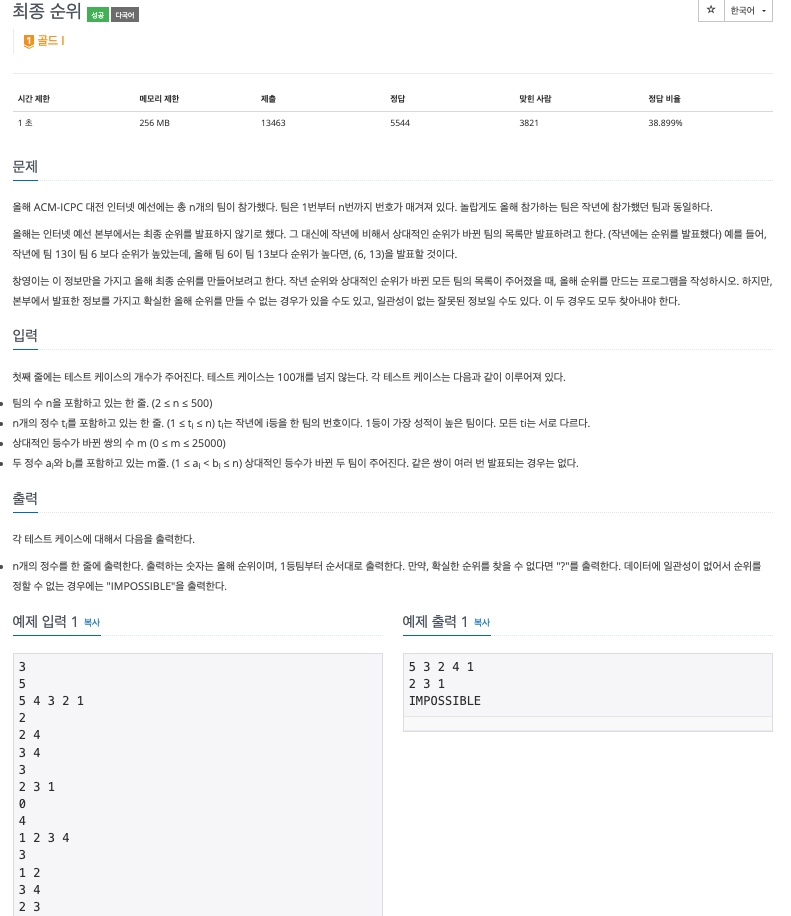
해당 문제는 위상 정렬의 특징을 공부하기 좋은 문제인 것 같다. 해당 문제에서 유의해야 할 점은 다음과 같다.
1. 그래프 간선 정의
- 초기 순위를 바탕으로 그래프를 직접 정의해야 한다.
- 예를 들어 초기 순위가 5 4 3 2 1일 경우를 가정해보자.
- 5 : 진입 차수가 0이며, 그래프에서 하위 노드로 4, 3, 2, 1이 추가되어야 한다.
- 4 : 진입 차수가 1이며, 그래프에서 하위 노드로 3, 2, 1이 추가되어야 한다.
- 바뀐 순위에 따라서 해당 관계를 역전시켜주어야 한다.
- 만약 4 > 2가 2 > 4로 바뀌는 경우를 가정해보자.
- 4의 하위 노드에서 2를 제거하고, 진입 차수를 증가시킨다.
- 2의 하위 노드에 4를 추가하고, 진입 차수를 감소시킨다.
2. 정보의 일관성(사이클) 확인 (IMPOSSIBLE)
- 상대적인 순위 변경 정보에 일관성이 없는 경우, 즉, 모순된 정보가 제공되면 올바른 위상 정렬이 불가능하다.
- 예를 들어 a > b와 b > a가 동시에 존재하는 경우이며. 이러한 모순은 그래프에서 사이클을 형성하게 된다.
3. 결과의 유일성 확인 (?)
- 위상 정렬 과정에서 특정 시점에 진입 차수가 0인 노드가 두 개 이상 존재한다면 여러 가지 가능한 순서가 존재한다는 것이다.
- 이 경우 정확한 하나의 순위를 결정할 수 없다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int test = Integer.parseInt(st.nextToken());
StringBuilder resultSb = new StringBuilder();
//각각의 테스트 케이스에 대해서
for(int t = 0 ; t < test; t++){
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
List<Integer>[] graph = new LinkedList[n+1];
st = new StringTokenizer(br.readLine());
int[] sequence = new int[n+1]; // 초기 노드들의 순서
// 그래프 초기화
for(int i = 1; i <= n; i++){
sequence[i] = Integer.parseInt(st.nextToken());
graph[i] = new LinkedList<>();
}
// 초기 진입 차수 계산 (5 4 3 2 1 이라면)
// 5 : 진입 차수가 0이며, 그래프에서 하위 노드로 4, 3, 2, 1이 추가되어야 한다.
// 4 : 진입 차수가 1이며, 그래프에서 하위 노드로 3, 2, 1이 추가되어야 한다.
int[] D = new int[n+1];
for(int i = 1; i <= n - 1; i++){
for(int j = i + 1; j <= n; j++){
graph[sequence[i]].add(sequence[j]);
D[sequence[j]]++;
}
}
st = new StringTokenizer(br.readLine());
int m = Integer.parseInt(st.nextToken());
// 바뀐 관계에 대해서 진입 차수와 그래프 갱신
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
Integer a = Integer.parseInt(st.nextToken());
Integer b = Integer.parseInt(st.nextToken());
// 이미 관계가 존재했을 때, 해당 관계를 역전시킨다.
if(graph[a].contains(b)){ //a의 하위 노드가 b였을 경우
graph[a].remove(b);
graph[b].add(a);
D[a]++;
D[b]--;
}
else if(graph[b].contains(a)){ //b의 하위 노드가 a였을 경우
graph[b].remove(a);
graph[a].add(b);
D[a]--;
D[b]++;
}
}
// 위상 정렬 수행
Queue<Integer> queue = new LinkedList<>();
boolean notFix = false;
for(int i = 1; i <= n; i++){
if(D[i] == 0){
queue.offer(i);
}
}
// 위상 정렬을 완료한 노드들의 수
int count = 0;
StringBuilder sb = new StringBuilder();
while(!queue.isEmpty()){
// 큐의 사이즈가 1을 초과할 경우 정렬 결과가 여러개일 수 있다는 뜻.
if(queue.size() > 1){
notFix = true;
}
int current = queue.poll();
sb.append(current).append(" ");
count++;
for(int next : graph[current]){
D[next]--;
if(D[next] == 0){
queue.offer(next);
}
}
}
// 모든 노드들이 위상 정렬을 수행하지 못했을 때에는 IMPOSSIBLE
if(count < n){
sb.setLength(0);
sb.append("IMPOSSIBLE").append("\n");
}
// 정렬 결과가 여러개일 수 있는 경우
else if(notFix){
sb.setLength(0);
sb.append("?").append("\n");
}
// 1개의 결과로 위상 정렬을 성공할 경우
else{
sb.append("\n");
}
resultSb.append(sb);
}
System.out.println(resultSb);
}
}
문제 : 선행 조건이 있을 경우 최소 비용 계산하기 (백준 1005, ACM Craft)
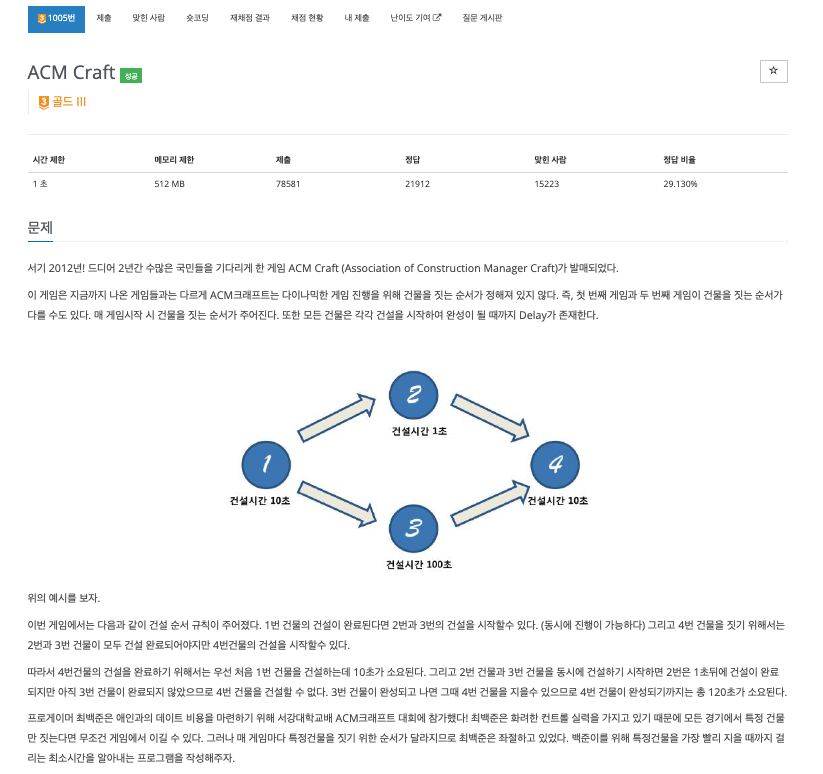
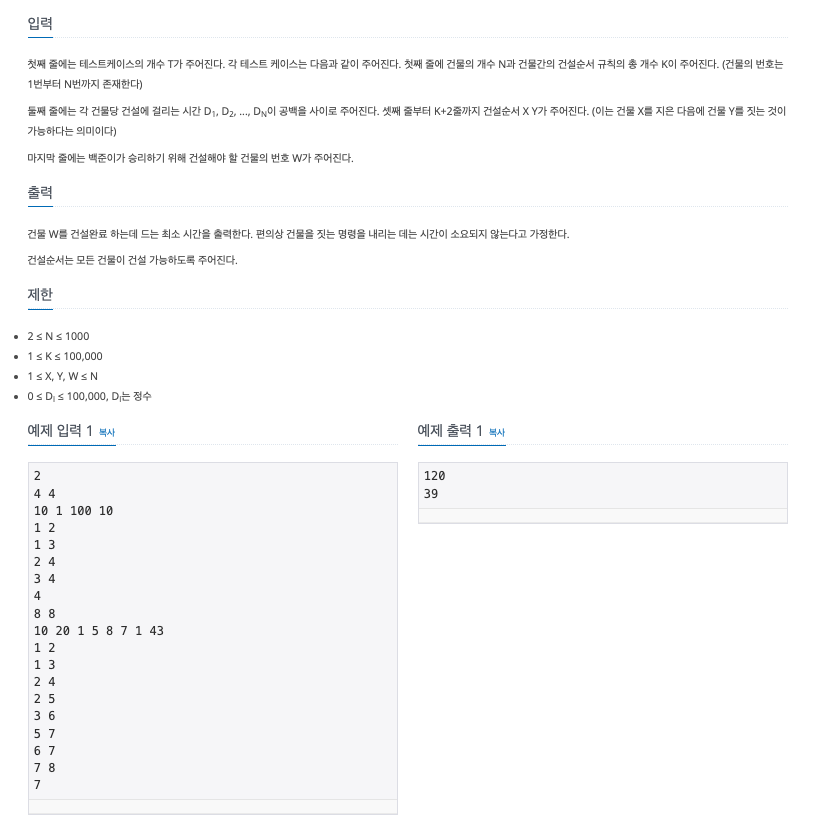
선행 조건이 있는 방향 그래프에서, 해당 노드의 모든 선행 조건을 완료하고 방문 가능한 최소 비용을 계산하는 문제이다.
해당 그래프를 위상 정렬을 수행해보면 "1 -> 2 -> 3 -> 4"가 될 것이다.
이 때, 4번 노드를 생각해보면 2와 3의 순위는 동일하므로 "1 -> 2 -> 4" 혹은 "1 -> 3 -> 4" 두 가지가 선행되어야 하고, 2번 노드와 3번 노드의 작업이 모두 수행되어야 4번 노드에 방문이 가능하므로 둘 중 최대값을 구해야 하는 문제이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
int test = Integer.parseInt(st.nextToken());
// 각 테스트 케이스마다
for(int t = 0; t < test; t++){
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[] cost = new int[n+1]; //비용을 저장할 배열
int[] D = new int[n+1]; // 위상 정렬을 위한 진입 차수 배열
// 그래프 초가화 및 비용 입력
List<Integer>[] graph = new LinkedList[n+1];
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= n; i++){
cost[i] = Integer.parseInt(st.nextToken());
graph[i] = new LinkedList<>();
}
// 진입 차수 배열 초기화와 그래프에 간선 추가
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
graph[a].add(b);
D[b]++;
}
long[] dp = new long[n+1]; // 누적된 비용을 저장할 배열
Arrays.fill(dp, Long.MIN_VALUE); // 최대값을 저장할 것이므로 초기에는 MIN값으로 설정
// 위상 정렬 수행
Queue<Integer> queue = new LinkedList<>();
for(int i = 1; i <= n; i++){
if(D[i] == 0){
queue.offer(i);
dp[i] = cost[i];
}
}
// 결과를 구해야 할 노드 인덱스 입력
st = new StringTokenizer(br.readLine());
int result = Integer.parseInt(st.nextToken());
while(!queue.isEmpty()){
int current = queue.poll();
if(current == result){ // 만약 결과 노드일 경우 위상 정렬을 중지해도 된다.
break;
}
for(int next : graph[current]){
D[next]--;
// 하위 노드들의 누적 비용을 "현재 노드의 누적 비용 + 하위 노드의 비용"과 비교하여 최대값으로 갱신
dp[next] = Math.max(dp[next], dp[current] + cost[next]);
if(D[next] == 0){
queue.offer(next);
}
}
}
sb.append(dp[result]).append("\n");
}
System.out.println(sb);
}
}
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 최소 신장 트리(MST) : 크루스칼(Kruskal) (0) | 2024.12.29 |
|---|---|
| [알고리즘/JAVA] 유니온 파인드 (Union-find, Disjoint-Set) (0) | 2024.08.10 |
| [알고리즘/JAVA] 그래프 최단경로 : Floyd-Warshall (플로이드-워셜) (0) | 2024.07.11 |
| [알고리즘/JAVA] 그래프 최단경로 : Bellman-Ford (벨만-포드) (2) | 2024.07.10 |
| [알고리즘/JAVA] 그래프 최단경로 : Dijkstra (다익스트라) (0) | 2024.07.08 |














