[알고리즘/JAVA] 그래프 최단경로 : Floyd-Warshall (플로이드-워셜)
2024. 7. 11. 18:56
반응형

플로이드 워셜( Floyd-Warshall)
가중치가 존재하는 그래프의 시작 정점으로부터 다른 정점들까지의 최단 거리를 구하는 알고리즘. 모든 정점 쌍 사이의의 최단 거리를 탐색한다.
특징
시작 정점으로부터 나머지 정점의 최단거리를 알아내는 다익스트라나 벨만-포드와 달리 모든 정점들 간의 거리를 탐색한다.
Edge 가중치가 음수일 경우에도 사용 가능 (단 음수 싸이클이 있으면 안됨)
시간 복잡도 : O(N^3) (N = 노드의 개수) → 노드의 개수가 200개 내외로 주어지는 경우에 사용을 고려할 수 있다.
동적 계획법을 활용하여 부분해를 활용하여 문제를 해결하는 방식을 사용한다.
- A -> B -> C의 최단 거리를 구할 때, A->B와, B->C의 최단 거리를 안다면, A->B->C의 최단 거리를 알 수 있다.
과정
초기화

- 각 정점 간의 초기 거리를 나타내는 행렬 D를 설정한다.
- 이 행렬의 D[i][j]는 초기 상태에서 정점 i에서 정점 j로 가는 경로의 가중치를 나타낸다.
- 만약 경로가 없으면 이 값을 무한대로 설정한다.
동적 프로그래밍을 이용한 거리 업데이트
- 세 개의 중첩된 반복문을 사용하여 모든 경유지 K, 출발 노드 S, 도착 노드 E에 대해 최단 경로를 계산한다.
for 경유지 K (1~N)
for 출발 노드 S (1~N)
for 도착 노드 E (1~N)
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])
- 점화식: D[S][E] = min(D[S][E], D[S][K]+ D[K][E])
- 경유지 K를 거쳐가는 경로와 직접 가는 경로 중 더 짧은 경로를 선택한다.

플로이드-워셜 구현 : 백준 11404 (플로이드)

정점 N의 개수가 100개 이하, 모든 도시의 쌍에 대해서 거리를 계산 : 플로이드 워셜을 사용하여 풀이할 수 있다.
import java.io.*;
import java.util.*;
public class Main {
// 정점의 개수 (도시의 수)
static int n;
// 간선의 개수 (버스의 수)
static int m;
// 거리 배열. distance[i][j]는 i에서 j로 가는 최단 거리를 저장
static long[][] distance;
// 무한대
static final long INF = 10000000000L;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
// 거리 배열 초기화
distance = new long[n+1][n+1];
for(long[] line : distance){
Arrays.fill(line, INF); // 모든 값을 무한대로 초기화
}
// 자기 자신으로 가는 거리는 0으로 초기화
for(int i = 1; i <= n; i++){
distance[i][i] = 0;
}
// 간선 정보를 입력받아 거리 배열에 저장
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 이미 있는 경로보다 짧은 경우만 갱신
distance[start][end] = Math.min(distance[start][end], weight);
}
// 플로이드-워셜
for(int k = 1; k <= n; k++){
for(int s = 1; s <= n; s++){
for(int e = 1; e <= n; e++){
// s에서 e로 가는 기존 거리와 s에서 k를 거쳐 e로 가는 거리를 비교하여 더 짧은 거리로 갱신
distance[s][e] = Math.min(distance[s][e], distance[s][k] + distance[k][e]);
}
}
}
StringBuilder sb = new StringBuilder();
for(int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// 무한대인 경우 0으로 출력
if(distance[i][j] == INF){
sb.append(0).append(" ");
}
else{
sb.append(distance[i][j]).append(" ");
}
}
sb.append("\n");
}
System.out.println(sb);
}
}
문제 : 백준 1956 (운동)
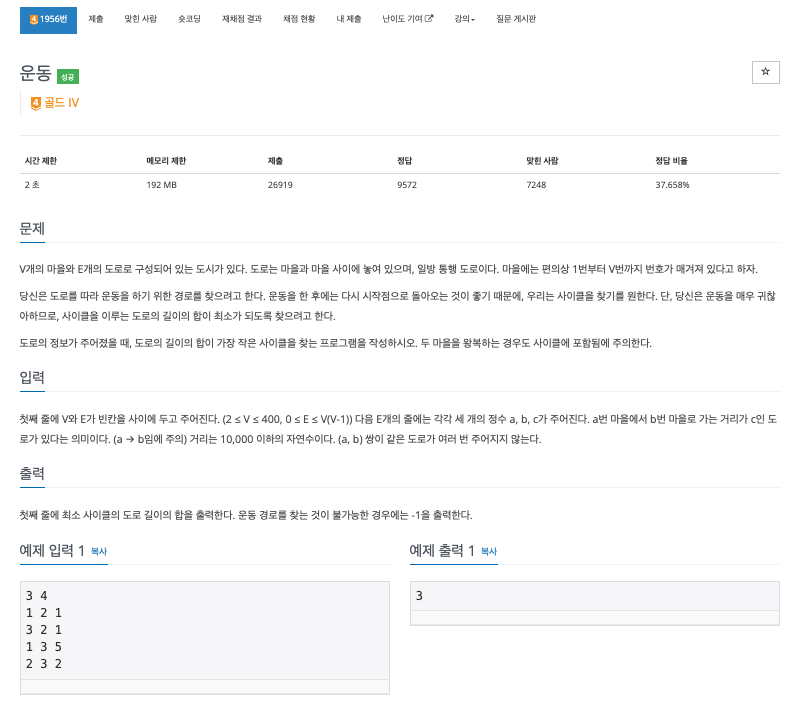
이번 문제도 마찬가지로 모든 정점에 대해서 최단 거리를 찾는 문제이다.
단, 싸이클 중 최소 거리를 찾아야 하므로, 시작 정점과 도착 정점이 모두 자신인 경우들 중 최소값을 구해야 한다.
따라서 초기 D 배열을 초기화 할 때, D[i][i]를 0으로 초기화하지 않고 INF로 초기화하여, 싸이클에 대한 거리를 계산할 수 있도록 한다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int n;
static int m;
static long[][] distance;
static final long INF = 10000000000L;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
distance = new long[n+1][n+1];
for(long[] line : distance){
Arrays.fill(line, INF);
}
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
distance[start][end] = Math.min(distance[start][end], weight);
}
for(int k = 1; k <= n; k++){
for(int s = 1; s <= n; s++){
for(int e = 1; e <= n; e++){
distance[s][e] = Math.min(distance[s][e], distance[s][k] + distance[k][e]);
}
}
}
long result = INF;
for(int i = 1; i <= n; i++){
result = Math.min(distance[i][i], result);
}
if(result == INF){
result = -1;
}
System.out.println(result);
}
}반응형
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 그래프 위상 정렬 (Topological Sort) (0) | 2024.08.11 |
|---|---|
| [알고리즘/JAVA] 유니온 파인드 (Union-find, Disjoint-Set) (0) | 2024.08.10 |
| [알고리즘/JAVA] 그래프 최단경로 : Bellman-Ford (벨만-포드) (2) | 2024.07.10 |
| [알고리즘/JAVA] 그래프 최단경로 : Dijkstra (다익스트라) (0) | 2024.07.08 |
| [알고리즘/JAVA] 그래프 탐색 : DFS / BFS (깊이우선 탐색 / 너비우선 탐색) (0) | 2024.05.27 |














