[알고리즘/JAVA] 그래프 최단경로 : Bellman-Ford (벨만-포드)
2024. 7. 10. 03:43
반응형

벨만-포드 (Bellman-Ford)
가중치가 존재하는 그래프의 시작 정점으로부터 다른 정점들까지의 최단 거리를 구하는 알고리즘 출발 노드로부터의 모든 노드의 최단 거리를 탐색한다.
활용
다익스트라와 달리 Edge의 가중치가 음수일 때도 사용 가능하다.
그래프에서 음수 사이클의 존재 여부를 판단하는 문제에 활용할 수 있다.
과정
그래프 구현
- 벨만 포드 알고리즘은 Edge를 중심으로 동작한다 -> 그래프를 Edge List로 구현

초기화
- 최단 거리 배열(D)를 초기화한다. 모든 정점의 최단 경로 값을 INF로 초기화, 시작 정점의 최단 경로 값을 0으로 설정
최단 거리 갱신
- 그래프의 모든 Edge에 대해 (정점 수 - 1)번 반복하여 최단 경로 값을 갱신.
- 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 정점 개수 - 1이다.
- 업데이트 방법 : D[s] ≠ INF, D[e] = max(D[e], D[s] + w)
- s = 출발 정점, e = 도착 정점
- [타겟 정점 e의 현재 거리]와 [시작 정점 s의 현재 거리 + 가중치 w]의 크기를 비교하여 작은 거리로 갱신한다.
- K번째 싸이클의 업데이트는 K개의 Edge를 사용했을 경우의 해당 정점까지의 최단 거리이다.


- 정점의 개수가 5개이므로 4번의 싸이클을 통해서 최단 거리 배열을 업데이트한다.
- 각 업데이트 시 Edge 배열에서 시작 정점의 거리가 INF가 아닌 간선들을 선택하여 업데이트한다.
- [타겟 정점 e의 현재 거리]와 [시작 정점 s의 현재 거리 + 가중치 w]의 크기를 비교하여 작은 거리로 갱신한다.
음수 사이클 확인
- (정점 수 - 1)번의 반복이 끝난 후에도 최단 경로 값이 갱신된다면 음수 사이클이 존재함을 알 수 있다.
- 음수 사이클이 존재한다는 것은 최단 거리를 찾을 수 없는 그래프라는 뜻을 의미한다.
요약
- 벨만-포드는 Edge 중심의 최단거리 탐색 알고리즘
- 최단거리 갱신 : N-1번의 업데이트
- 음수 싸이클 판단 : 한번 더 업데이트를 하여 업데이트가 된다면 최단거리 X, 음수 싸이클이 존재
벨만-포드 구현 : 백준 11657 (타임머신)
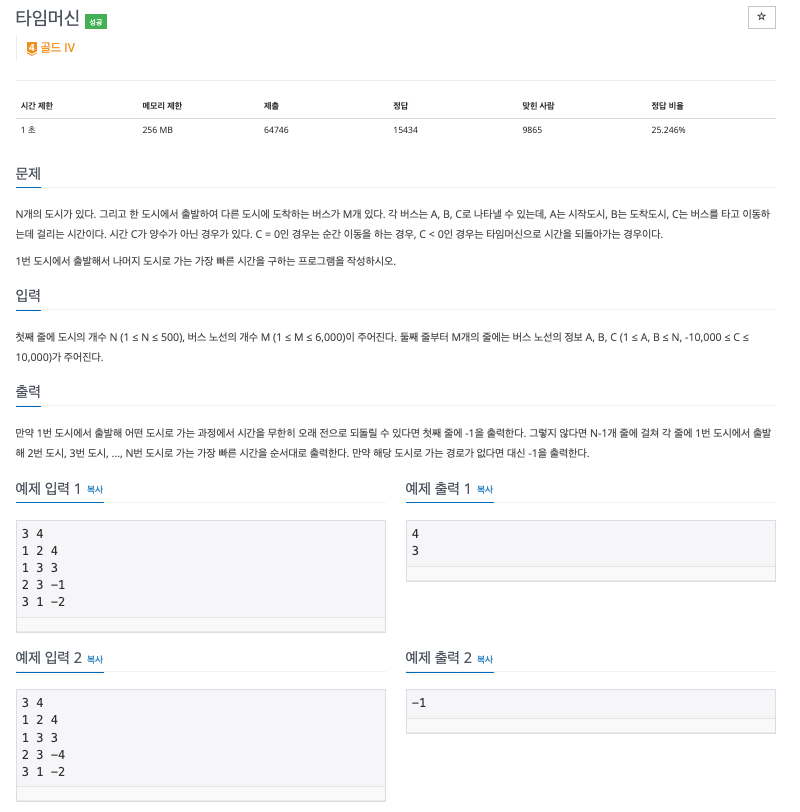
"시작 정점으로부터 각 정점까지의 최단 거리", "가중치가 음수", "음수 사이클 판단" -> 벨만 포드 사용을 기억하자.
- "1번 도시에서 출발하여 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램"-> 시작 정점으로부터 각 정점까지의 최단 거리
- "C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우"-> 가중치가 음수
- "어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면"-> 음수 사이클 판단
유의할 점은 최단거리 배열(distance)의 자료형을 너무 작게 하거나 INF의 값을 작게 준다면 틀릴 수 있으니 유의하자.
import java.io.*;
import java.util.*;
public class Main {
static int n; // 정점의 개수
static int m; // 간선의 개수
static int[][] graph; // 간선 정보를 저장하는 2차원 배열 (시작 정점, 끝 정점, 가중치)
static long[] distance; // 시작 정점으로부터 각 정점까지의 최단 거리를 저장하는 배열
static final int INF = 2000000000; // INF
/**
* 벨만-포드 알고리즘을 사용하여 최단 경로를 찾는 함수
* @param start 시작 정점
* @return 음수 사이클이 있으면 true, 없으면 false
*/
static boolean bellmanFord(int start){
Arrays.fill(distance, INF); // 모든 정점의 최단 거리 값을 무한대로 초기화
distance[start] = 0; // 시작 정점의 최단 거리 값을 0으로 설정
// 모든 간선에 대해 (정점 수 - 1)번 반복하여 최단 거리 값을 갱신
for(int i = 0; i < n - 1; i++){
for(int j = 0; j < m; j++){
// 간선의 시작 정점이 방문된 정점인 경우에만 갱신
if(distance[graph[j][0]] != INF){
// 기존의 최단 거리 값과 새로운 경로를 통한 거리 값을 비교하여 더 작은 값으로 갱신
distance[graph[j][1]] = Math.min(distance[graph[j][1]], distance[graph[j][0]] + graph[j][2]);
}
}
}
// 음수 사이클 존재 여부를 확인
boolean isCycle = false;
for(int j = 0; j < m; j++){
// 여전히 갱신할 수 있는 경우, 음수 사이클이 존재함을 의미
if(distance[graph[j][0]] != INF && distance[graph[j][1]] > distance[graph[j][0]] + graph[j][2]){
isCycle = true;
break;
}
}
return isCycle; // 음수 사이클 존재 여부 반환
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); // 입력을 받기 위한 BufferedReader 객체 생성
StringTokenizer st = new StringTokenizer(br.readLine()); // 첫 번째 줄 입력 (정점의 개수와 간선의 개수)
n = Integer.parseInt(st.nextToken()); // 정점의 개수
m = Integer.parseInt(st.nextToken()); // 간선의 개수
graph = new int[m][3]; // 간선 정보를 저장할 배열 초기화
distance = new long[n+1]; // 최단 거리 값을 저장할 배열 초기화
// 간선 정보 입력
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
graph[i][0] = Integer.parseInt(st.nextToken()); // 시작 정점
graph[i][1] = Integer.parseInt(st.nextToken()); // 끝 정점
graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치
}
StringBuilder sb = new StringBuilder(); // 결과 출력을 위한 StringBuilder 객체 생성
// 음수 사이클 존재 시 -1 출력
if(bellmanFord(1)){
sb.append(-1);
} else {
// 각 정점에 대한 최단 거리 값을 출력
for(int i = 2; i <= n; i++){
long result = distance[i] == INF ? -1 : distance[i];
sb.append(result).append("\n");
}
}
System.out.println(sb); // 결과 출력
}
}
반응형
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 유니온 파인드 (Union-find, Disjoint-Set) (0) | 2024.08.10 |
|---|---|
| [알고리즘/JAVA] 그래프 최단경로 : Floyd-Warshall (플로이드-워셜) (0) | 2024.07.11 |
| [알고리즘/JAVA] 그래프 최단경로 : Dijkstra (다익스트라) (0) | 2024.07.08 |
| [알고리즘/JAVA] 그래프 탐색 : DFS / BFS (깊이우선 탐색 / 너비우선 탐색) (0) | 2024.05.27 |
| [자료구조/JAVA] 그래프 (Graph) (0) | 2024.05.27 |














