[알고리즘/JAVA] 그래프 탐색 : DFS / BFS (깊이우선 탐색 / 너비우선 탐색)

그래프(Graph)
그래프는 정점들과, 정점들을 연결하는 간선들로 구성된 자료 구조이다.
최단 경로 찾기, 네트워크 구성, 검색 엔진, 스케줄링 등 다양한 분야의 컴퓨터 과학에서 응용되어 사용되고 있다.
그래프 탐색
그래프 구조에서 정점(Vertex)과 간선(Edge)을 따라 이동하는 과정이다.
그래프 탐색는 주로 시작 정점에서 출발하여 인접한 정점을 탐색하는 방법을 사용하며, 그 종류는 다음과 같다.
- 깊이 우선 탐색(DFS, Depth-First Search): 가능한 한 깊숙한 곳까지 이동한 후 다시 돌아와 다음 가능한 경로를 탐색한다.
- 너비 우선 탐색(BFS, Breadth-First Search): 시작 정점에서 가까운 정점부터 차례로 방문하며 넓게 탐색한다.
시작 정점이 1일 때 두 가지 방법의 방문 순서는 다음과 같다.

DFS의 정점 방문 순서
1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 > 9 > 10 > 11 > 12
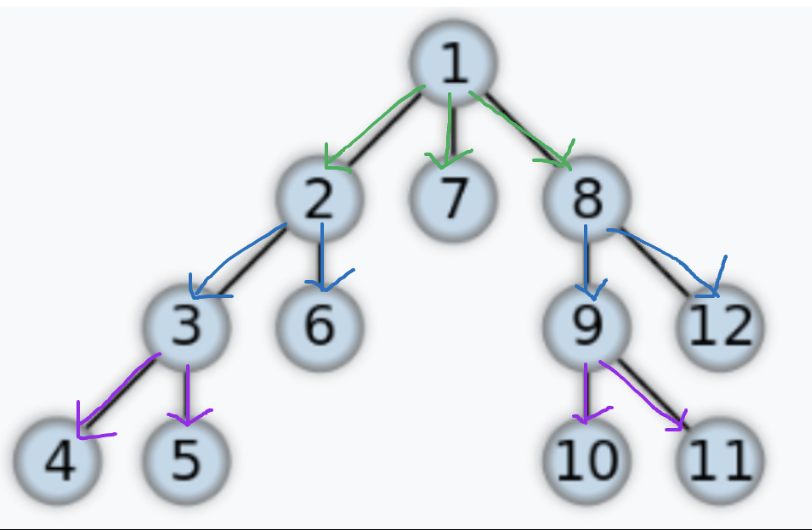
BFS의 정점 방문 순서
1 > 2 > 7 > 8 > 3 > 6 > 9 > 12 > 4 > 5 >10 > 11
https://en.wikipedia.org/wiki/Depth-first_search
그래프 표현
이전 포스팅에서 다루었던 인접 행렬을 이용해서 그래프를 우선 표현해주었다.
https://sjh9708.tistory.com/221
[자료구조/JAVA] 그래프 이론 (Graph Theory)
그래프(Graph) 그래프는 정점들과, 정점들을 연결하는 간선들로 구성된 자료 구조이다. 최단 경로 찾기, 네트워크 구성, 검색 엔진, 스케줄링 등 다양한 분야의 컴퓨터 과학에서 응용되어 사용되
sjh9708.tistory.com
public class Graph {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("정점의 개수 입력:");
int n = scanner.nextInt();
int[][] adjMat = new int[n][n];
System.out.print("간선의 수 입력:");
int e = scanner.nextInt();
System.out.print("간선 N줄 입력(u->v) (예시 : 1 2):");
for (int i = 0; i < e; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
adjMat[u][v] = 1;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(adjMat[i][j] + " ");
}
System.out.println();
}
System.out.print("BFS 시작 정점 입력 :");
int start = scanner.nextInt();
bfs(adjMat, start);
System.out.print("DFS 시작 정점 입력 :");
int start = scanner.nextInt();
dfs(adjMat, start);
}
}
다음 인접 행렬은 다음의 그래프를 표현한 것이다. (정점 0은 사용하지 않도록 간선을 누구와도 연결하지 않았다 )


깊이 우선 탐색(DFS) 구현
static void dfs(int[][] adjMat, int startV) {
int n = adjMat.length;
boolean[] visited = new boolean[n];
Stack<Integer> stack = new Stack<>();
System.out.println("탐색 시작 : " + startV);
stack.push(startV);
while (!stack.isEmpty()) {
int vertex = stack.pop();
if(visited[vertex] == false){
visited[vertex] = true;
System.out.print(vertex + " ");
for (int i = n - 1; i >= 0; i--) {
if (adjMat[vertex][i] == 1 && !visited[i]) {
stack.push(i);
}
}
}
}
System.out.println();
}- adjMat : 정점들 간의 연결 관계를 나타내는 인접 행렬이며, startV는 탐색을 시작할 정점의 인덱스이다.
- visited : 방문을 완료한 정점을 기록할 배열이다.
- stack : 방문할 정점들을 담기 위한 Stack이다. DFS는 최대한 깊이 방문해야 하므로 LIFO 구조인 스택을 사용한다.
- 스택을 사용해서 탐색 중에 이전에 방문한 정점을 기록하고, 최대한 깊이 탐색한 후 더 이상 탐색할 정점이 없을 경우 백트래킹하여 이전 경로로 돌아갈 수 있다.
과정
- 시작 정점을 스택에 넣은 후 해당 정점으로부터 탐색을 시작한다.
- 스택이 비어있을 때까지 아래 과정을 반복한다.
- 스택에서 정점을 하나 꺼내서 해당 정점을 출력한다.
- 방문하지 않은 정점이라면 방문 완료 표시를 한다.
- 인접 행렬을 통해 해당 정점과 연결된 모든 정점을 확인한다.
- 인접 행렬에서 해당 정점과 연결된 정점은 1로 표시된다.
- 해당 정점들 중 방문하지 않은 정점이 있으면 그 정점을 스택에 넣는다.
- 스택이 비어있으면 탐색이 완료되었으므로 함수를 종료한다.
DFS 시작 정점 입력 :1
탐색 시작 : 1
1 2 3 4 5 6 7 8 9 10 11 12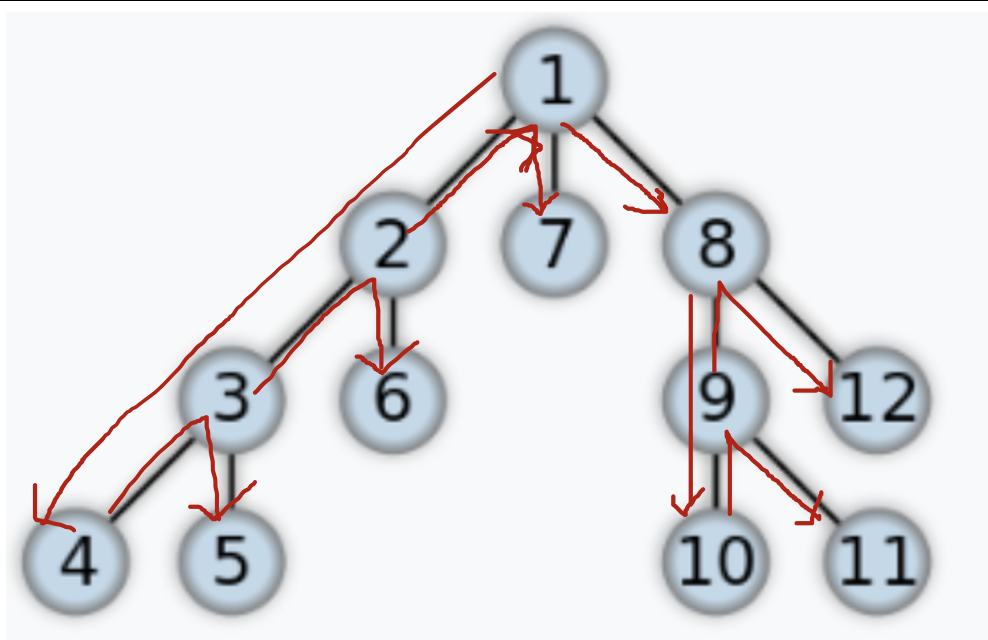
너비 우선 탐색(BFS) 구현
static void bfs(int[][] adjMat, int startV) {
int n = adjMat.length;
boolean[] visited = new boolean[n];
Queue<Integer> queue = new LinkedList<>();
System.out.println("탐색 시작 : " + startV);
queue.add(startV);
visited[startV] = true;
while (!queue.isEmpty()) {
int vertex = queue.poll();
System.out.print(vertex + " ");
for (int i = 0; i < n; i++) {
if (adjMat[vertex][i] == 1 && !visited[i]) {
queue.add(i);
visited[vertex] = true;
}
}
}
System.out.println();
}- adjMat : 정점들 간의 연결 관계를 나타내는 인접 행렬이며, startV는 탐색을 시작할 정점의 인덱스이다.
- visited : 방문을 완료한 정점을 기록할 배열이다.
- queue : 방문할 정점들을 담기 위한 Queue이다. BFS는 최대한 시작 정점으로부터 인접하게, 즉 넓게 방문해야 하므로 FIFO 구조인 스택을 사용한다.
- BFS는 한 레벨의 모든 정점을 탐색한 후 그 다음 레벨의 정점을 탐색한다. 따라서 탐색할 정점들을 순서대로 처리하기에 큐가 적합하다.
과정
- 시작 정점을 큐에 넣은 후 해당 정점으로부터 탐색을 시작한다.
- 큐가 비어있을 때까지 아래 과정을 반복한다.
- 큐에서 정점을 하나 꺼내서 해당 정점을 출력한다.
- 인접 행렬을 통해 해당 정점과 연결된 모든 정점을 확인한다.
- 인접 행렬에서 해당 정점과 연결된 정점은 1로 표시된다.
- 해당 정점들 중 방문하지 않은 정점이 있으면 그 정점을 큐에 넣고 방문 표시를 한다.
- 큐가 비어있으면 탐색이 완료되었으므로 함수를 종료한다.
BFS 시작 정점 입력 :1
탐색 시작 : 1
1 2 7 8 3 6 9 12 4 5 10 11
탐색 알고리즘 비교
방문 표시 시점 (visited)
DFS는 스택에서 노드를 Pop할 때 방문 표시를 한다.
LIFO 구조이기 때문에, 스택에 노드를 Push할 때 방문 표시를 미리 해두게 된다면, 최근에 추가된 노드를 먼저 탐색해야 하는데 이미 방문 처리가 되어서 탐색이 불가능해진다.
- 예를 들어, 노드 A에서 B로 가는 경로와 C에서 B로 가는 경로가 차례로 있을 때, B는 두 번 스택에 Push된다.
- 만약 Push할 때 방문 표시를 진행하고 중복 노드가 Push되지 못하게 한다면, C->B를 먼저 탐색해야 하는데 A->B로 방문 표시가 이미 되어 있는 상태라 깊이우선 탐색이 불가능하다.
- 따라서 Pop될 때 방문 표시를 진행하여 C->B의 탐색이 완료되면, B의 탐색 완료 표시를 하고, A->B를 탐색하지 않게 하는 것이 DFS를 구현하기 적절하다.
BFS는 큐에 노드를 Push할 때 방문 표시를 한다.
- 같은 노드를 여러 번 큐에 넣는 것을 방지하기 위해서이다. 어차피 레벨 수준의 순서대로 탐색을 진행하기 때문에 중복된 노드가 들어갈 필요가 없다.
- 노드 A에서 B로 가는 경로와 C에서 B로 가는 경로가 차례로 있을 때, B는 A->B 과정으로 탐색이 순서대로 먼저 진행되면, C->B에서는 탐색을 진행할 필요가 없다.
- 따라서 Enqueue하는 시점에서 방문 표시를 하는 것이 큐에 중복으로 노드가 들어가는 것을 방지할 수 있다.
DFS는 LIFO이기 때문에 중복으로 노드를 Push하는 것을 구조상 허용해야 한다. 대신 마지막으로 Push된 노드의 탐색만 진행하도록 방문 처리를 하면 된다.
반면 BFS는 FIFO이기 때문에 처음부터 중복으로 노드를 Push하는 것을 막을 수 있다.
사용 목적
1. DFS : 경로의 존재 여부를 판단, 그래프의 모든 경로를 탐색, 싸이클 탐지 등을 할 때 유용하다.
2. BFS : 가중치가 없는 그래프의 최단 경로를 탐색할 때 유용하다. 일반적으로 DFS보다 탐색 성능이 좋다.
3. 다익스트라 : 가중치 그래프에서의 최단 경로를 탐색할 때 사용된다.
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 그래프 최단경로 : Bellman-Ford (벨만-포드) (2) | 2024.07.10 |
|---|---|
| [알고리즘/JAVA] 그래프 최단경로 : Dijkstra (다익스트라) (0) | 2024.07.08 |
| [자료구조/JAVA] 그래프 (Graph) (0) | 2024.05.27 |
| [알고리즘/JAVA] 그리디와 우선순위 큐 (과제, 강의실 배정, 보석 도둑) (0) | 2024.05.27 |
| [알고리즘/JAVA] 이진 탐색 : 개념 (수 찾기, 랜선 자르기) - Upper/Lower Bound (0) | 2024.05.06 |














