[알고리즘/JAVA] 분할 정복법 : 개념 (합병 정렬, 행렬 제곱, 색종이)

분할 정복법 (Divide and conquer)
큰 규모의 문제를 풀기 위해 하위 문제로 나누어 풀이하고 이들의 해답을 결합하여 최종 해답을 얻는 방법이다.
문제를 가장 작은 단위의 문제로 분할한 후, 해당 문제들을 결합하여 부분 해답을 도출, 또 다시 부분 해답을 결합하는 과정을 통해서 최종적으로 큰 규모의 문제를 풀이한다.
분할 정복법의 과정
1. 분할(Divide): 해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나눈다.
2. 정복(Conquer): 나눈 작은 문제를 각각 해결한다.
3. 통합(Combine): (필요하다면) 해결된 해답을 모은다.
분할 정복법의 조건
1. 문제의 분할이 쉽게 가능해야 한다.
- 주어진 문제를 작은 부분 문제들로 나눌 수 있어야 한다.
- 또한 문제를 분할하는 과정이 너무 복잡하거나 비효율적이면 분할 정복법을 적용하기 어렵다.
2. 하위 문제를 해결하는 방식이 상위 문제를 해결하는 방식과 동일해야 한다
- 재귀적으로 동일한 방식을 통해서 하위 문제를 해결한다는 아이디어를 사용하므로. 하위 문제를 해결하는 방식이, 상위 문제를 해결하는 방식과 동일해야 한다.
3. 부분 문제의 해결이 독립적이고 효율적이어야 한다.
- 하나의 부분 문제를 해결하는 과정이 다른 부분 문제의 결과에 영향을 주지 않아야 한다.
- 부분 문제를 해결하는데 너무 많은 시간이 소요된다면 전체 문제를 해결하는데도 많은 시간이 걸릴 수 있다.
DP(동적 프로그래밍)과 분할 정복법
DP와 분할 정복법은 문제를 하위 문제로 나누어 풀이한다는 아이디어는 동일하다.
그렇지만 DP에서는 하위 문제들이 독립되지 않고, 다른 문제들의 풀이에 재사용된다는 점에서 차이가 있다.
또한 분할 정복법에서는 모든 하위 문제들의 결합이 전체 문제의 해가 되지만, 동적 프로그래밍에서는 일부 필요한 하위 문제들의 해결을 통해서 전체 문제를 해결한다.
합병 정렬로 보는 분할 정복법
분할 정복법의 대포적인 예시로 합병 정렬이 있다. 분할 정복법의 과정을 중심으로 한번 살펴보자.

1. 분할(Divide)
배열을 두 개의 균등한 크기로 분할한다. 재귀적으로 수행되며 더 이상 분할할 수 없을 때까지 분할을 반복한다.
2. 정복(Conquer)
분할된 각 부분에 대해 재귀적으로 배열을 정렬한다.
3. 병합(Combine)
정렬된 두 개의 부분 배열을 병합하여 하나의 정렬된 배열로 만든다.
<함께 보기> 정렬 알고리즘
https://sjh9708.tistory.com/209
[알고리즘/JAVA] 정렬 알고리즘 : 선택, 삽입, 버블, 병합, 퀵 정렬
정렬 정렬 알고리즘에 대한 연구는 컴퓨터 과학자들 사이에서 오래 전 부터 이루어져 왔다.그 과정에서 많은 정렬 알고리즘들이 탄생했는데, 그 중 잘 알려진 정렬 알고리즘 몇몇개를 살펴 보
sjh9708.tistory.com
문제 : 행렬 제곱 (백준 10830)
분할 정복법 문제로 유명한 행렬 제곱 알고리즘이다.
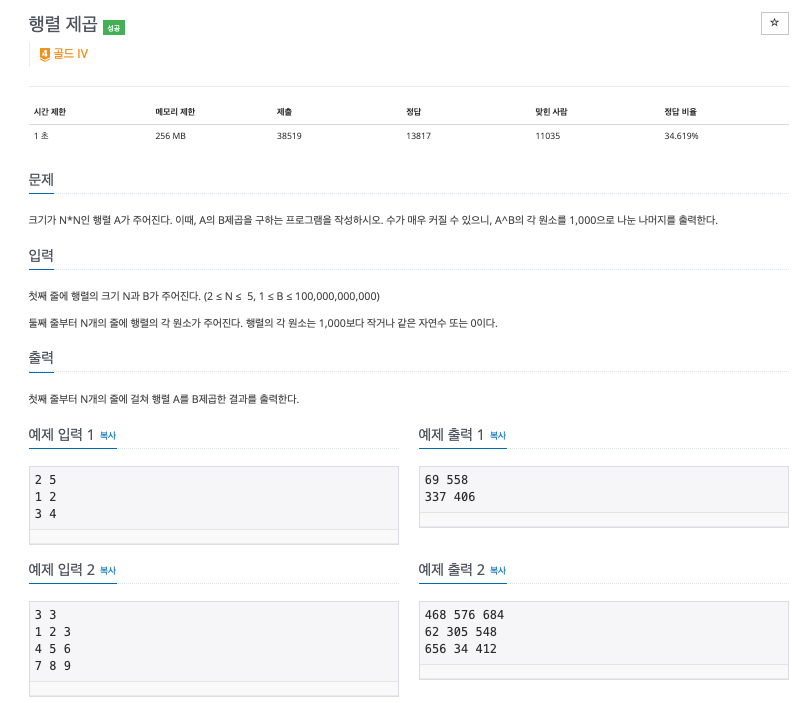
행렬의 제곱
만약 행렬 A를 4제곱한다고 하면 AxAxAxA의 연산을 거친다. 하지만 이는 (AxA)x(AxA)로도 표현 가능하다.
즉 A^4 = (A^2) * (A^2)로 표현이 가능해진다.
이를 토대로 A^7를 분할 정복 관점으로 표현해보자.
A^7 = (A^4) x (A^3)
- A^4 = (A^2) x (A^2)
- A^3 = (A^2) x A
- A^2 = A x A
A^7 = (((AxA) x (AxA)) x ((AxA) x A))
즉 행렬의 제곱은 행렬의 곱셈이라는 하위 문제로 분할하여 표현이 가능하다는 소리이다.
구현
행렬 곱셈 연산
static int n;
static long[][] A;
static long[][] calc(long[][] a, long[][] b){
long[][] R = new long[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
long sum = 0;
for(int l = 0; l < n; l++){
sum += (a[i][l] * b[l][j]) % 1000;
}
R[i][j] = sum % 1000;
}
}
return R;
}
행렬 A x A를 수행하는 함수를 작성해주자.
문제 조건에 따라서, A의 범위를 long으로 설정해 주어야 한다는 점과, 너무 큰 수에 대해서 1000으로 나눈 나머지를 사용하라는 조건이 있으므로, 연산 중간중간에 1000을 넘어가지 않는 범위가 되도록 모듈러 연산을 수행해 주어야 한다.
행렬 제곱 연산
static long[][] square(long b){
if(b == 1){
return A;
}
// Divide : 두 개의 부분 하위 제곱으로 표현하기 위한 연산
long[][] P = square(b / 2); //부분 하위 제곱 P
// Conquer : 부분 하위 제곱들로 상위 제곱 문제 해결
if(b % 2 == 0){
//짝수의 경우 : P x P
return calc(P, P);
}
else{
//홀수의 경우 : P x (PxP)
return calc(A, calc(P, P));
}
}
행렬 제곱 연산에서 큰 제곱 문제를 두 개의 하위 제곱 문제로 표현해야 한다. 예를 들어 A^6 = A^3 x A^3으로 표현되어야 하고, A^3은 A^2 x A로 표현되어야 한다.
따라서 들어온 제곱 계수를 2로 나눈 값에 대해서 제곱 연산을 재귀적으로 호출한다.
제곱 계수에 따라서 홀수와 짝수의 케이스를 나누어 주어야 한다. 문제를 부분 문제로 Divide할 때 2로 나누어주기 때문에 홀수의 경우에는 추가적으로 연산이 필요하기 때문이다. 아래는 예시이다.
- square(4)라면 calc(square(2), square(2))
- square(5)라면 calc(calc(square(2), square(2)), A)
만약 제곱 계수가 1이라면 행렬 A를 그대로 리턴시키는 것이 답이므로 재귀문의 종료 조건으로서 사용한다.
전체 코드
public class Main {
static int n;
static long[][] A;
static long[][] calc(long[][] a, long[][] b){
long[][] R = new long[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
long sum = 0;
for(int l = 0; l < n; l++){
sum += (a[i][l] * b[l][j]) % 1000;
}
R[i][j] = sum % 1000;
}
}
return R;
}
static long[][] square(long b){
if(b == 1){
return A;
}
// 하위 제곱 연산의 결과
long[][] P = square(b / 2);
if(b % 2 == 0){
//짝수의 경우 : P x P
return calc(P, P);
}
else{
//홀수의 경우 : P x (PxP)
return calc(A, calc(P, P));
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
long b = Long.parseLong(st.nextToken());
A = new long[n][n];
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
for(int j = 0; j < n; j++){
A[i][j] = Long.parseLong(st.nextToken()) % 1000;
}
}
long[][] R = square(b);
StringBuilder sb = new StringBuilder();
for(long[] line : R){
for(long i : line){
sb.append(i).append(" ");
}
sb.append("\n");
}
System.out.println(sb);
}
}
문제 : 색종이 (백준 2630)

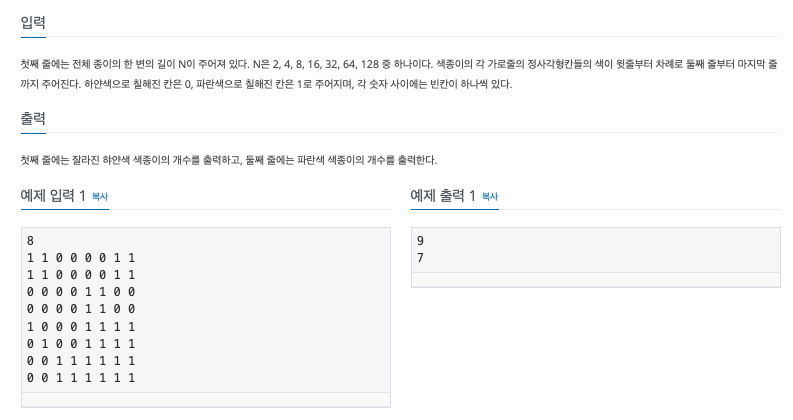
해당 문제를 간단히 말하자면 우선, 0(하얀색)과 1(파란색)로 나누어진 배열이 있다. 종이를 같은 색으로만 이루어진 작은 종이가 될 때 까지 계속해서 + 형태로 4등분하여 잘라 간다. 이 때 나올 수 있는 종이의 개수들을 출력하는 것이다.
구현
static int blue = 0;
static int white = 0;
static int check(int[][] array, int startX, int startY, int endX, int endY){
//종이의 맨 처음 시작과 색이 일치하지 않는 부분이 있다면 -1 반환
for(int i = startY; i <= endY; i++){
for(int j = startX; j <= endX; j++){
if(array[i][j] != array[startY][startX]){
return -1;
}
}
}
//모두 일치한다면 종이의 색 반환 (0 or 1)
return array[startY][startX];
}
static void split(int[][] array, int startX, int startY, int endX, int endY){
// 현재 분할된 종이의 색이 모두 일치하는지 체크
int ck = check(array, startX, startY, endX, endY);
if(ck == 1){
blue++;
}
else if(ck == 0){
white++;
}
// 모두 일치하지 않는다면 4등분으로 분할
else{
int midX = startX + ((endX - startX) / 2);
int midY = startY + ((endY - startY) / 2);
split(array, startX, startY, midX, midY);
split(array, midX + 1, startY, endX, midY);
split(array, startX, midY + 1, midX, endY);
split(array, midX + 1, midY + 1, endX, endY);
}
}
해당 메서드는 현재 부분 배열의 요소(색)가 모두 일치하는지 확인하고, 그렇지 않으면 4등분으로 나누어 해당 메서드를 재귀적으로 수행하는 함수이다.
check() 메서드는 종이의 색이 모두 일치한다면 해당 색(파란색 1, 하얀색 0)을 반환하고, 그렇지 않다면 -1을 반환한다.
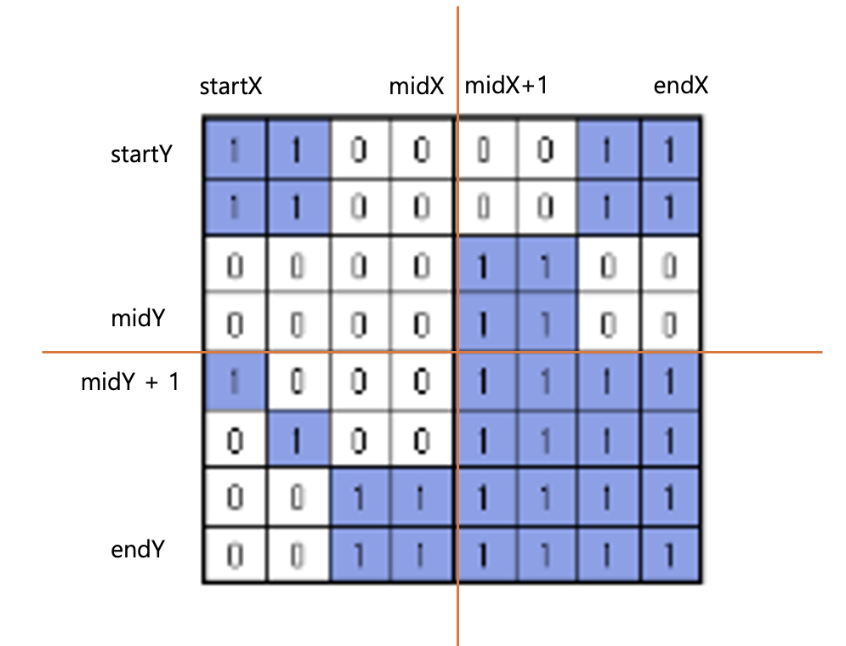
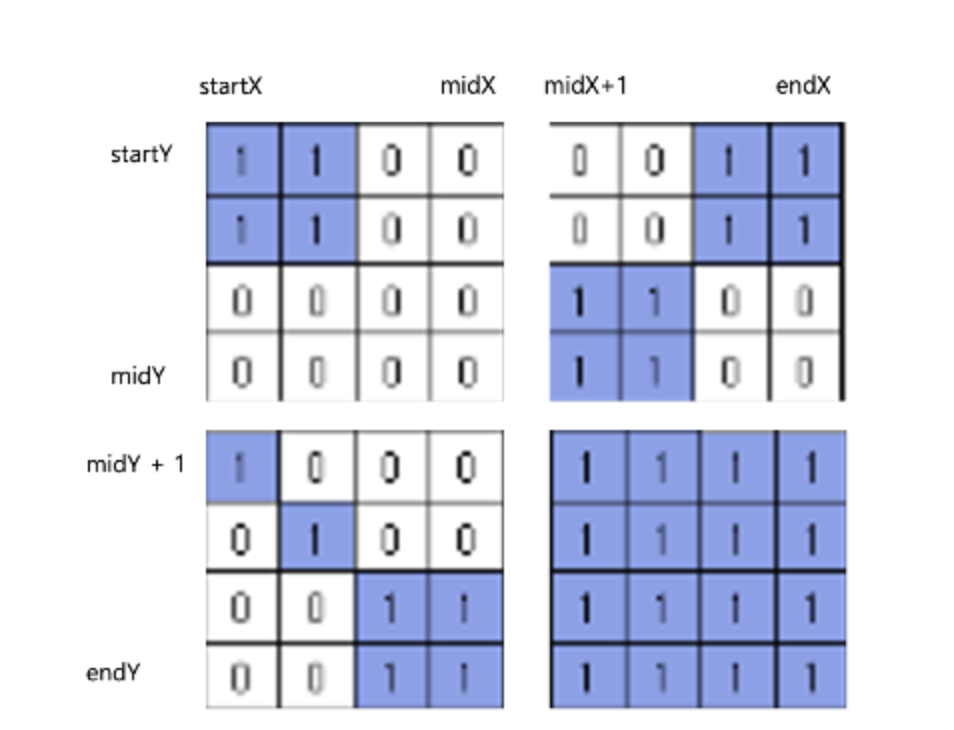
분할하는 방식은 다음과 같다. 인덱스를 통해 각각 x(가로), y(세로)의 중간 지점을 얻어내어 분할 지점을 계산한다.
위의 종이는 startX의 인덱스가 0이고, endX의 인덱스가 7이다. 따라서 midX는 3이고, midX + 1은 4이다.
Y도 마찬가지로 계산될 것이다. 이를 기반으로 종이(start(0,0), end(7,7))은 아래 네 개의 종이로 분할될 수 있다.
- start(0,0), end(3,3)
- start(3,0), end(7,3)
- start(0,3), end(3,7)
- start(3,3), end(7,7)

분할된 종이에서 또 다시 위의 방식을 문제가 해결될 때 까지 재귀적으로 호출한다.
Conquer되는 과정에서는 문제 조건에 따라서 해결된 문제들, 즉 색이 같은 종이의 수를 합산하기만 하면 된다.
전체 코드
public class Main {
static int blue = 0;
static int white = 0;
static int check(int[][] array, int startX, int startY, int endX, int endY){
//종이의 맨 처음 시작과 색이 일치하지 않는 부분이 있다면 -1 반환
for(int i = startY; i <= endY; i++){
for(int j = startX; j <= endX; j++){
if(array[i][j] != array[startY][startX]){
return -1;
}
}
}
//모두 일치한다면 종이의 색 반환 (0 or 1)
return array[startY][startX];
}
static void split(int[][] array, int startX, int startY, int endX, int endY){
// 현재 분할된 종이의 색이 모두 일치하는지 체크
int ck = check(array, startX, startY, endX, endY);
if(ck == 1){
blue++;
}
else if(ck == 0){
white++;
}
// 모두 일치하지 않는다면 4등분으로 분할
else{
int midX = (startX + endX) / 2;
int midY = (startY + endY) / 2;
split(array, startX, startY, midX, midY);
split(array, midX + 1, startY, endX, midY);
split(array, startX, midY + 1, midX, endY);
split(array, midX + 1, midY + 1, endX, endY);
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int[][] array = new int[n][n];
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
for(int j = 0; j < n; j++){
array[i][j] = Integer.parseInt(st.nextToken());
}
}
split(array, 0, 0, n-1, n-1);
System.out.println(white);
System.out.println(blue);
}
}
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 그리디와 우선순위 큐 (과제, 강의실 배정, 보석 도둑) (0) | 2024.05.27 |
|---|---|
| [알고리즘/JAVA] 이진 탐색 : 개념 (수 찾기, 랜선 자르기) - Upper/Lower Bound (0) | 2024.05.06 |
| [알고리즘/JAVA] 그리디 (Greedy) : 개념 (동전, 단어 수학, 허프만 코딩) (0) | 2024.05.01 |
| [알고리즘/JAVA] 동적 계획법(DP) : LIS (최장 증가 부분 수열) (0) | 2024.05.01 |
| [알고리즘/JAVA] 동적 계획법(DP) : 배낭 채우기 문제 (0-1 Knapsack) (0) | 2024.04.30 |













