[알고리즘/JAVA] 정렬 알고리즘 : 선택, 삽입, 버블, 병합, 퀵 정렬

정렬
정렬 알고리즘에 대한 연구는 컴퓨터 과학자들 사이에서 오래 전 부터 이루어져 왔다.
그 과정에서 많은 정렬 알고리즘들이 탄생했는데, 그 중 잘 알려진 정렬 알고리즘 몇몇개를 살펴 보려고 한다. 살펴볼 것은 아래와 같다.
시간 복잡도가 O(n^2)인 정렬 : 버블 정렬, 삽입 정렬, 선택 정렬
시간 복잡도가 O(nlog(n))인 정렬 : 병합 정렬(항상), 퀵 정렬(일반적으로)
참고로 자바에서 내장되어 있는 Arrays.sort() 메서드는 다음 정렬 알고리즘을 사용한다.
- 퀵 정렬: 퀵정렬 중 이중 피벗 퀵정렬을 사용한다.
- 병합 정렬: JDK 6까지 주로 사용되었으며, 아직 남아있는 부분이 있다.
여담으로 현재 가장 많이 사용되고 있는 정렬 알고리즘은 퀵 정렬, 병합 정렬, 힙 정렬 정도가 있다.
그렇다면 나머지 정렬들을 알아야 하는 이유는 무엇일까? 내 생각에는 같은 요구사항을 구현하기 위해서 이렇게 다양한 알고리즘이 사용될 수 있다는 것을 보여주는 대표적인 예시이자, 컴퓨터 과학자들의 고뇌를 알 수 있는 사례인 것 같다.
우리는 이를 통해 알고리즘에 대한 통찰력과 사고력을 키울 수 있을 것이다.
선택 정렬 : Selection Sort

가장 단순한 형태의 정렬 알고리즘 중 하나이다.
1. 맨 앞부터 차례대로 정렬할 대상 인덱스로 설정하고 아래의 싸이클에 따라 정렬한다.
2. 정렬할 인덱스의 해당 값을 포함한 이후의 값들 중 최소값을 찾아낸다.
3. 그 값을 정렬할 인덱스의 값과 Swap한다.
4. 정렬된 인덱스의 다음 인덱스를 대상 인덱스로 설정하고 해당 과정을 끝까지 반복한다.
https://ko.wikipedia.org/wiki/%EC%84%A0%ED%83%9D_%EC%A0%95%EB%A0%AC
구현
public class SelectionSort {
static void print(int arr[]){
for(int k : arr){
System.out.print(k + " ");
}
System.out.println();
}
static void swap(int arr[], int i, int j){
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
static void sort(int arr[]){
for(int i = 0; i < arr.length - 1; i++){
print(arr);
int min = i; // 현재 사이클에서 최소값
for(int j = i + 1; j < arr.length; j++){
if(arr[j] < arr[min]){
min = j;
}
}
swap(arr, i, min);
}
}
public static void main(String[] args) {
int[] array = {6, 5, 3, 1, 8, 7, 2, 4};
sort(array);
print(array);
}
}
6 5 3 1 8 7 2 4
1 5 3 6 8 7 2 4
1 2 3 6 8 7 5 4
1 2 3 6 8 7 5 4
1 2 3 4 8 7 5 6
1 2 3 4 5 7 8 6
1 2 3 4 5 6 8 7
1 2 3 4 5 6 7 8
다음 수행 결과를 살펴보면 앞쪽부터 차례대로 정렬이 이루어 지는 것을 확인할 수 있다.
삽입 정렬 : Insertion Sort
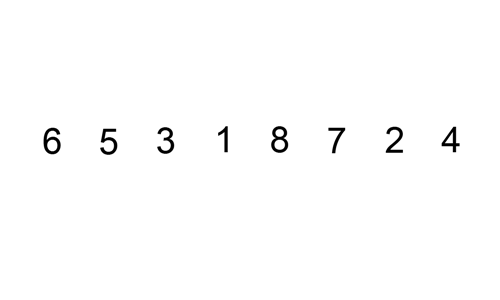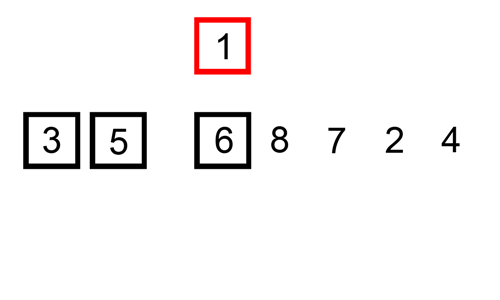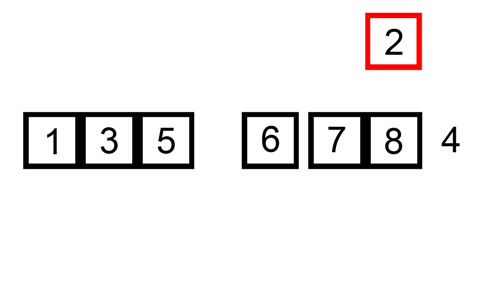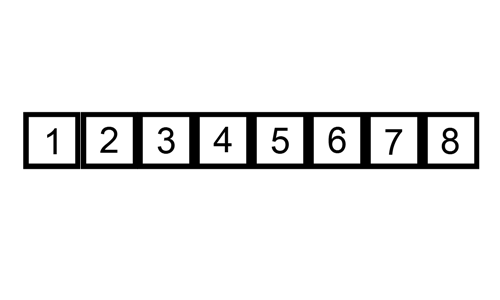
삽입 정렬은 앞에서부터 차례대로 이미 정렬된 배열에서 적당한 위치를 찾아서 끼워넣는 알고리즘을 사용한다. 인류가 숫자 카드를 정렬하는 방법과 가장 유사하다.
1. 두 번째 값부터 마지막 값까지 차례로 아래의 사이클을 따라 정렬을 시작한다. (첫 번째 값은 비교할 정렬된 배열이 없으므로 수행하지 않아도 된다.)
2. 정렬 대상을 대상의 왼쪽 원소와 비교하여, 만약 왼쪽 원소가 더 크다면 위치를 교환한다.
3. 이를 반복하다 왼쪽 원소가 더 크지 않으면 해당 자리가 해당 원소가 정렬되어 들어갈 자리인 것이다.
구현
public class InsertionSort {
static void print(int arr[]){
for(int k : arr){
System.out.print(k + " ");
}
System.out.println();
}
static void swap(int arr[], int i, int j){
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
static void sort(int arr[]){
for(int i = 1; i < arr.length; i++){
print(arr);
int target = i; // 현재 사이클에서 정렬할 대상
for(int j = i - 1; j >= 0; j--){
if(arr[target] < arr[j]){
swap(arr, target, j);
target = j; // 타겟을 이동시킨 지점으로 타겟위치 지정
}
}
}
}
public static void main(String[] args) {
int[] array = {6, 5, 3, 1, 8, 7, 2, 4};
sort(array);
print(array);
}
}
6 5 3 1 8 7 2 4
5 6 3 1 8 7 2 4
3 5 6 1 8 7 2 4
1 3 5 6 8 7 2 4
1 3 5 6 8 7 2 4
1 3 5 6 7 8 2 4
1 2 3 5 6 7 8 4
1 2 3 4 5 6 7 8
다음 수행 결과를 살펴보면 정렬 대상 인덱스의 앞쪽 배열이 정렬된 형태로 생성되어지고 있다.
버블 정렬 : Bubble Sort
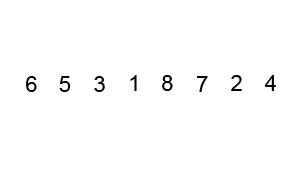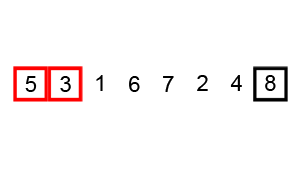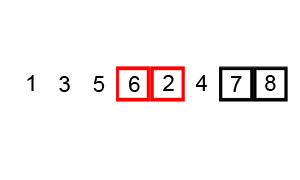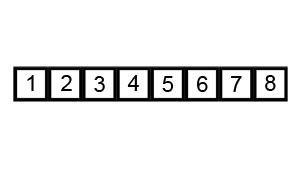
버블 정렬은 가장 무식하게 정렬하는 방법이라고 생각한다. 알고리즘은 다음과 같다.
1. 맨 앞부터 시작하여, 인접한 값과 비교하여 큰 값은 뒤로, 작은 값은 앞으로 보낸다.
2. 해당 과정을 거치면 맨 뒤에는 가장 큰 값이 위치할 것이다.
3. 뒤쪽의 정렬된 값을 제외하고 나머지에 대해서 같은 과정을 수행하여 전체 배열에 대한 정렬을 수행한다.
구현
public class BubbleSort {
static void print(int arr[]){
for(int k : arr){
System.out.print(k + " ");
}
System.out.println();
}
static void swap(int arr[], int i, int j){
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
// 끝부터 차례로 정렬된다.
static void sort(int arr[]){
for(int i = 0; i < arr.length - 1; i++){
print(arr);
for(int j = 0; j < arr.length -i - 1; j++){
if(arr[j] > arr[j + 1]){
swap(arr, j, j+ 1);
}
}
}
}
public static void main(String[] args) {
int[] array = {6, 5, 3, 1, 8, 7, 2, 4};
sort(array);
print(array);
}
}
6 5 3 1 8 7 2 4
5 3 1 6 7 2 4 8
3 1 5 6 2 4 7 8
1 3 5 2 4 6 7 8
1 3 2 4 5 6 7 8
1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8
다음 수행 결과를 살펴보면 뒤쪽 인덱스부터 차례대로 정렬이 이루어지는 것을 확인할 수 있다.
합병 정렬 : Merge Sort
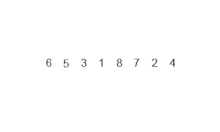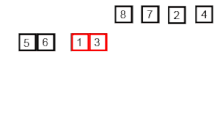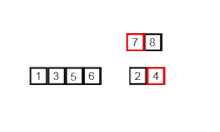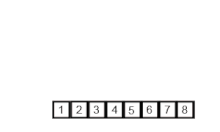
합병 정렬은 분할 정복법의 알고리즘을 사용하고 있으며, 아래 세 단계의 알고리즘을 거쳐서 정렬이 이루어진다.
1. 분할(Divide): 배열을 두 개의 균등한 크기로 분할한다. 재귀적으로 수행되며 더 이상 분할할 수 없을 때까지 분할을 반복한다.
2. 정복(Conquer): 분할된 각 부분에 대해 재귀적으로 합병 정렬을 통해 배열을 정렬한다.
3. 병합(Combine): 정렬된 두 개의 부분 배열을 병합하여 하나의 정렬된 배열로 만든다.
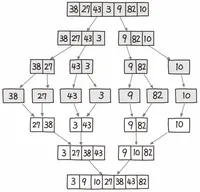
다음 그림으로 다시 살펴보자.
1. 배열의 원소 개수가 1 또는 0이 될 때 까지 계속해서 쪼갠다.
2. 분할된 두 부분 배열들을 정렬하면서 합친다.
3. 이는 재귀적으로 이루어지며, 모든 부분 배열들이 병합될 때 까지 반복한다.
구현
public class MergeSort {
static void print(int arr[], int left, int right){
for(int i = 0; i < arr.length; i++){
if(i == left){
System.out.print("[");
}
System.out.print(arr[i]);
if(i == right){
System.out.print("] ");
}
else{
System.out.print(" ");
}
}
System.out.println();
}
static void merge(int arr[], int left, int mid, int right){
int[] left_arr = Arrays.copyOfRange(arr, left, mid + 1);
int[] right_arr = Arrays.copyOfRange(arr, mid + 1, right + 1);
int i = 0; //왼쪽 배열 검사 인덱스
int j = 0; //오른쪽 배열 검사 인덱스
int k = left; //합병중인 배열의 현재 인덱스
while (i < left_arr.length && j < right_arr.length) {
if (left_arr[i] <= right_arr[j]) {
arr[k++] = left_arr[i++];
}
else {
arr[k++] = right_arr[j++];
}
}
while (i < left_arr.length) {
arr[k++] = left_arr[i++];
}
while (j < right_arr.length) {
arr[k++] = right_arr[j++];
}
print(arr, left, right);
}
static void mergeSort(int[] arr, int left, int right){
//left와 right로 분할 가능하다면
if(left < right){
int mid = (right + left) / 2; //mid
//mid를 기준으로 두 파트로 분할
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right); //분할한 결과 합병 (분할 정복)
}
}
static void sort(int arr[]){
mergeSort(arr, 0, arr.length - 1);
}
public static void main(String[] args) {
int[] array = {6, 5, 3, 1, 8, 7, 2, 4};
print(array, -1, -1);
sort(array);
}
}
6 5 3 1 8 7 2 4
[5 6] 3 1 8 7 2 4
5 6 [1 3] 8 7 2 4
[1 3 5 6] 8 7 2 4
1 3 5 6 [7 8] 2 4
1 3 5 6 7 8 [2 4]
1 3 5 6 [2 4 7 8]
[1 2 3 4 5 6 7 8]
위의 출력 결과를 살펴보면 맨 처음 6, 5, 3, 1, 8, 7, 2, 4로 분할되어 시작된다.
그리고 왼쪽부터 재귀적으로 차례로 병합과 동시에 정렬을 수행한다. [ ]에 있는 값들이 현재 사이클에서 정렬되어 병합된 값들이다.
참고로 병합을 수행할 때의 정렬 방식은 다음과 같다. 위 코드에서는 merge()에서 이루어진다.
[1 3 5 6] [2 4 7 8] -> []
[1 3 5 6] [2 4 7 8] -> [1]
[1 3 5 6] [2 4 7 8] -> [1, 2]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3, 4]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3, 4, 5]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3, 4, 5, 6]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3, 4, 5, 6, 7]
[1 3 5 6] [2 4 7 8] -> [1, 2, 3, 4, 5, 6, 7, 8]
퀵 정렬 : Quick Sort : 고정값 Pivot 사용
퀵 정렬은 평균적인 상황에서 가장 좋은 성능을 가지는 정렬 알고리즘이다. 그렇지만 알고리즘에서 사용되는 피봇을 어떻게 설정하느냐에 따라서 성능이 달라질 수 있다.
퀵 정렬 또한 분할 정복법의 알고리즘을 사용한다.
1. 분할(Divide): 배열에서 하나의 요소를 선택하여 이를 pivot으로 정하고 pivot을 기준으로 pivot보다 작은 요소는 pivot의 왼쪽으로, pivot보다 큰 요소는 pivot의 오른쪽으로 이동시킨다.
2. 정복(Conquer): pivot을 기준으로 분할된 두 개의 부분 배열에 대해 재귀적으로 퀵 정렬을 수행한다. 부분 배열의 크기가 1 이하가 되어 더이상 정렬을 할 수 없을 때 까지 재귀적으로 반복한다.
3. 결합(Combine): 모든 정렬된 부분 배열을 결합하여 최종적으로 정렬된 배열을 얻는다.
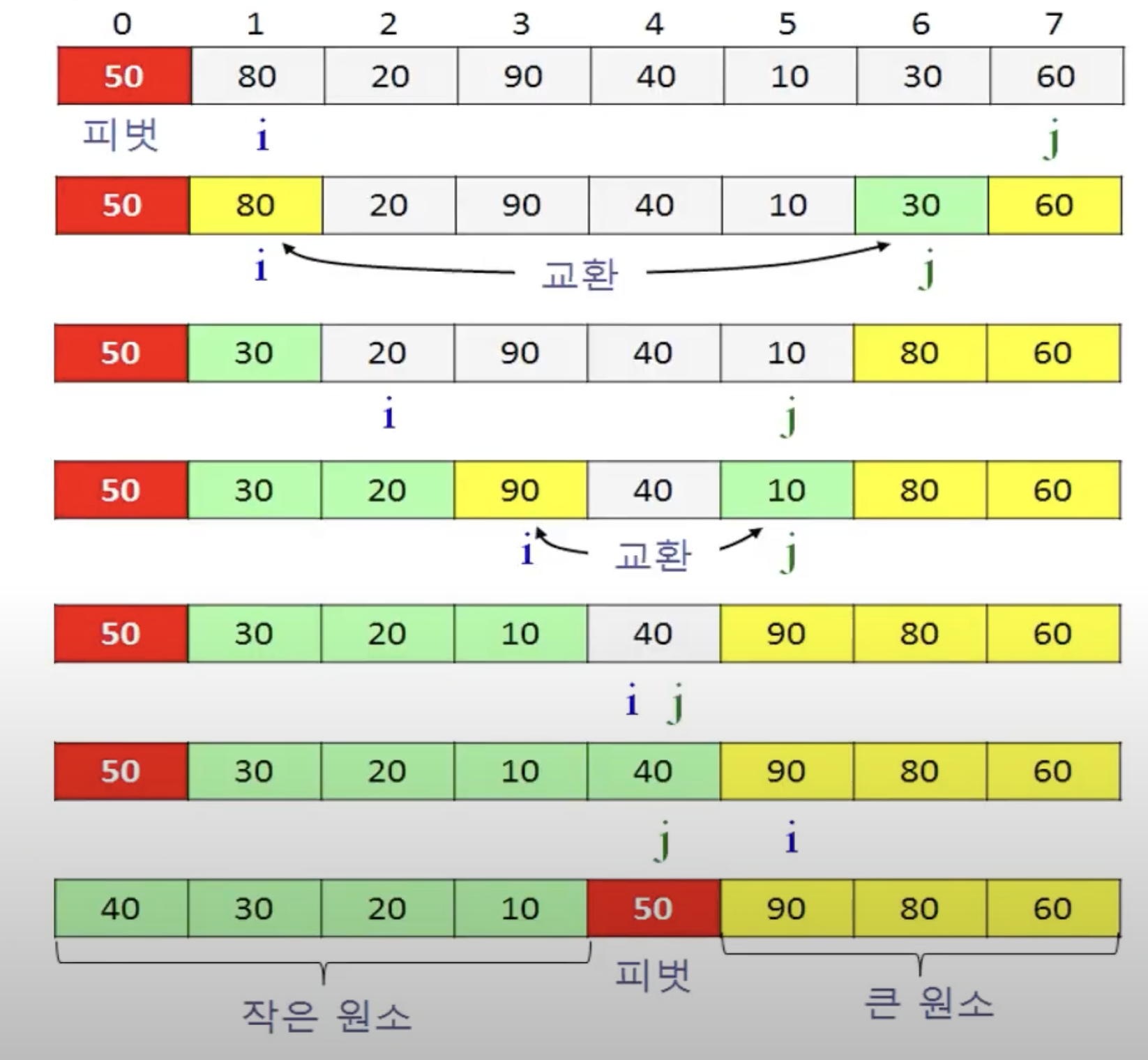
아래의 그림은 위의 알고리즘의 한 사이클이다.
Pivot 설정 : 랜덤 피봇이나, 중앙값 피봇, 이중 피봇, 하이브리드 피봇 등 다양한 방식이 있지만 가장 단순한 형태는 배열의 앞쪽 혹은 뒤쪽 인덱스를 Pivot으로 삼는 것이다.
해당 방법은 고정값 피봇이라고 하여, 가장 구현하기 쉽지만 최악의 경우 O(n^2)의 시간 복잡도를 가질 수 있다. 이를 위해서 위에서 언급한 다양한 피봇 설정 방식들이 연구되었다.
정렬 : 원소 하나를 기준(Pivot)으로 삼으면서, 그것보다 작은 값들은 배열의 앞쪽으로, 큰 값들은 배열의 뒤쪽으로 밀어넣는다.
- 피벗을 제외하고 배열의 첫 지점을 left(i), 마지막 지점을 right(j)로 설정하고, left는 순방향으로, right는 역방향으로 탐색을 진행한다.
- left는 피벗보다 큰 값을 찾을 것이고, right는 피벗보다 작은 값을 찾을 것이다. 왜냐하면 목적이 앞쪽에는 작은 값들이, 뒤쪽에는 큰 값들이 나열되게 하기 위해서이다.
- 만약 해당 값들을 찾았다면 left와 right의 해당 값들을 교환해준다.
- 만약 left가 right를 넘어선다면, 해당 경계의 값과 피벗 값을 교환한다.
Pivot 값을 적절한 위치에 삽입 : 정렬된 배열에서 작은 값들과 큰 값들의 경계에 Pivot값을 삽입한다. Pivot이 삽입된 위치를 기준으로 앞쪽에는 작은 값들이, 뒤쪽에는 큰 값들이 나열되게 된다.
재귀 : 피봇의 왼쪽과 오른쪽 부분 배열들에 대해서 똑같은 과정을 수행한다.
구현
public class QuickSort {
static void print(int arr[], int left, int right, int pivot){
for(int i = 0; i < arr.length; i++){
if(i == left){
System.out.print("[");
}
if(i == pivot){
System.out.print("*");
}
System.out.print(arr[i]);
if(i == right){
System.out.print("] ");
}
else{
System.out.print(" ");
}
}
System.out.println();
}
static void swap(int arr[], int i, int j){
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
static int partition(int[] arr, int low, int high) {
int left = low;
int right = high - 1;
//배열의 끝 인덱스를 pivot으로 설정
int pid = high;
int pivot = arr[pid];
//left 인덱스가 right 인덱스를 넘어가기 전까지 루프 진행
while(left <= right){
//Pivot의 왼쪽에는 작은 값이, 오른쪽에는 큰 값이 오도록 정렬하기 위해서 조건에 맞지않는 원소들을 찾아내서 교환할 것임
while(left <= high && arr[left] < pivot){
left++; //pivot보다 큰 값이 나올 때까지 -> 방향으로 이동
}
while(right >= low && arr[right] > pivot){
right--; //pivot보다 작은 값이 나올 때 까지 <- 방향으로 이동
}
//left와 right가 역전되지 않았고, 교환할 원소들을 찾았을 때
if(left <= right){
swap(arr, left, right);
}
}
// left right 위치가 역전되면 left와 pivot의 위치를 교환 -> Pivot의 왼쪽에는 작은 값이, 오른쪽에는 큰 값이 오도록 정렬됨
swap(arr, pid, left);
return left; // 변경된 Pivot의 위치(left) 반환
}
static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pivot = partition(arr, low, high); // 퀵 정렬 Phase를 통해 정렬된 Pivot의 위치
print(arr, low, high, pivot);
quickSort(arr, low, pivot - 1); // Pivot의 왼쪽을 다시 퀵 정렬 (Pivot보다 작은 값들임)
quickSort(arr, pivot + 1, high); // Pivot의 오른쪽을 다시 퀵 정렬 (Pivot보다 큰 값들임)
}
}
static void sort(int arr[]){
quickSort(arr, 0, arr.length - 1);
}
public static void main(String[] args) {
int[] array = {4, 2, 1, 8, 5, 7, 9, 6, 3};
print(array, 0, array.length - 1, -1);
sort(array);
print(array, 0, array.length - 1, -1);
}
}[4 2 1 8 5 7 9 6 3]
[1 2 *3 8 5 7 9 6 4]
[1 *2] 3 8 5 7 9 6 4
1 2 3 [*4 5 7 9 6 8]
1 2 3 4 [5 7 6 *8 9]
1 2 3 4 [5 *6 7] 8 9
[1 2 3 4 5 6 7 8 9]
[]는 현재 partition()이 이루어지고 있는 배열이며, *는 정렬된 피벗의 위치를 나타내는 것이다.
- [4 2 1 8 5 7 9 6 3]의 배열이 주어졌고 3을 피벗으로 선택한다.
- 3을 기준으로 왼쪽 부분 배열과 오른쪽 부분 배열 [1 2 *3 8 5 7 9 6 4]로 분할한다.
- [1 2] 부분 배열에서 2를 피벗으로 선택하여 정렬한다.
- [1 2] 부분 배열은 정렬 완료. [4 5 7 9 6 8] 부분 배열에서 8을 피벗으로 선택하여 정렬한다.
- 1 2 3 4 [5 7 6 *8 9]로 분할되었다. 다시 [5 7 6] 부분 배열에서 6을 피벗으로 선택하여 정렬한다
- [5 7 6] 부분 배열이 [5 6 7]로 정렬되었다. [9] 부분 배열은 정렬할 필요가 없다.
- 모든 부분 배열이 정렬되었다.
퀵 정렬 : Quick Sort : 중간값 Pivot 사용
퀵 정렬이 최악의 성능을 발휘하는 경우는 정렬 완료, 혹은 거의 정렬된 배열의 경우를 들 수 있다.
해당 경우에는 피벗이 고정되어 있으므로, 정렬 상태에 따라서 최악의 성능을 발휘할 수 있다.
중간값을 피벗으로 선택하게 되면 이런 최악의 경우까지는 안 갈 수 있도록 보장하며, 배열의 초기 정렬 상태에 성능이 좌우되는 것을 완화할 수 있다. 따라서 평균적인 성능의 향상을 기대할 수 있다.
static void quickSort(int[] array, int low, int high) {
if (low < high) {
int mid = low + (high - low) / 2;
threeSort(array, low, mid, high);
if(high - low + 1 > 3){
swap(array, mid, high);
int pivot = partition(array, low, high);
quickSort(array, low, pivot - 1);
quickSort(array, pivot + 1, high);
}
}
}
static void threeSort(int [] arr, int front, int mid, int rear){
if(arr[front] > arr[mid]) swap(arr, front, mid);
if(arr[mid] > arr[rear]) swap(arr, mid, rear);
if(arr[front] > arr[mid]) swap(arr, front, mid);
}
기존의 퀵 정렬과 달라지는 부분은 위와 같다.
우선 low, high, 그리고 해당 위치들의 중앙의 mid 세 곳을 검사하여 우선적으로 정렬한다.
- 만약 부분 배열이 3개 이하의 값일 경우 : 위의 과정으로 정렬이 완료되었으므로 별도의 partition() 과정을 하지 않는다.
- 만약 부분 배열이 4개 이상의 값일 경우 : 중간값에 해당하는 정렬된 mid에 위치한 값을 pivot으로 삼아서 partition을 수행한다. 기존 작성했던 로직이 high를 피봇으로 삼았으므로, mid와 high의 값을 스왑해준 후 수행한다.
Quick sort
총 소요된 시간: 50밀리초
중간값 Quick Sort
총 소요된 시간: 1밀리초
거의 정렬되어 있는 최악의 케이스, 10000 크기의 데이터로 실험해 보았을 때 유의미한 성능 차이를 보이는 것을 알 수 있다.
성능 : 병합 정렬 vs 퀵 정렬
퀵 정렬은 평균적으로 병합 정렬에 대해서 성능이 좋지만 최악의 경우를 고려해야 한다. 여러가지 Pivot을 설정하는 방법들을 제시하면서 성능을 개선할 수는 있지만, 결국 최악의 경우가 발생할 것을 상정하고 사용해야 한다.
따라서 일반적으로는 병합 정렬보다는 빠르지만, 운이 좋지 않으면 더 느려질 수 있다는 말이다.
또한 동일한 값에 대한 순서가 유지되지 않을 수 있는 Unstable(안정되지 않은) 정렬 방식이다.
병합 정렬은 퀵 정렬에 비해 평균적으로 느리고 추가적인 메모리 공간이 필요하다. 그렇지만 항상 nlog(n)의 시간 복잡도를 보장한다.
동일한 값에 대한 순서를 유지하는 Stable(안정된) 정렬 방식이다.
해당 문제는 백준 2751번 문제이다.
다음과 같은 백준 문제를 생각하면 알 수 있다. PS 사이트는 최악의 입력 케이스를 상정하는 경우가 있기 때문에 유의해야 한다.
입력값이 100만이라는 것은, nlogn일 때는 600만이지만, log(n^2)이 되면 1조개의 연산을 수행해야 한다.
일반적으로 시간제한 1초라는 뜻은, 많아봐야 1억개 미만의 연산을 뜻하므로 log(n^2)가 되는 케이스는 절대로 만들면 안된다는 소리이다.
실제로 해당 문제를 중간값 퀵 정렬과, 병합 정렬로 시도해보면 병합 정렬만이 모든 테스트 케이스를 통과하는 것을 알 수 있다.
Java에서 제공하는 정렬
Arrays.sort(array);
Collections.sort(list);
Arrays.sort(): 배열을 정렬하는 데 사용되는 방법이다. 퀵 정렬과 병합 정렬을 결합한 듀얼 피벗(Dual-Pivot) 퀵 정렬을 사용한다.
- 삽입 정렬과 퀵 정렬을 합친 형태이며, 작은 배열에 대해서는 삽입 정렬을, 큰 배열에 대해서는 퀵 정렬을 사용하는 방식이다.
- 평균적으로는 O(nlog(n))의 시간 복잡도이지만, 드물게 O(n^2)의 최악의 경우가 발생할 수 있다는 것은 퀵 정렬과 동일하다.
Collections.sort() : 컬렉션을 정렬하는 데 사용되는 방법이다. 합병 정렬과 삽입 정렬을 결합한 Timsort를 사용한다.
- 합병 정렬의 최악의 경우와, 삽입 정렬의 최선의 경우를 얻을 수 있는 방법이라고 보면 되고, 시간복잡도는 O(n) ~ O(nlogn)을 보장할 수 있다.
함께 보기
https://sjh9708.tistory.com/198
[Java] 정렬(Sorting) : Comparator과 Comparable
정렬 Java에서 배열과 컬렉션과 같은 데이터의 집합을 정렬하는 방법들에 대해서 살펴보겠다. 기본적인 정렬 방법부터, Comparator과 Comparable의 개념과, 둘의 사용 목적에 대해서 살펴보려고 한다.
sjh9708.tistory.com
정리
삽입 정렬 (Insertion Sort)
- 시간 복잡도: 평균 및 최악의 경우 : O(n^2)
- Stable 방식 : 동일한 값에 대한 순서가 유지된다.
선택 정렬 (Selection Sort)
- 시간 복잡도: 항상 O(n^2)
- Unstable 방식 : 동일한 값에 대한 순서가 유지되지 않을 수 있다
버블 정렬 (Bubble Sort)
- 시간 복잡도: 평균 및 최악의 경우 : O(n^2)
- Stable 방식 : 동일한 값에 대한 순서가 유지된다.
합병 정렬(Merge Sort)
- 시간 복잡도 : 평균 및 최악의 경우 : O(n log n)
- Stable 방식 : 동일한 값에 대한 순서가 유지된다.
퀵 정렬(Quick Sort)
- 시간 복잡도 : 평균 O(n log n), 최악의 경우 O(n^2)
- Unstable 방식 : 동일한 값에 대한 순서가 유지되지 않을 수 있다
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 동적 계획법(DP) : 개념 (파도반 수열 / 1로 만들기 / 계단 오르기) (0) | 2024.04.16 |
|---|---|
| [알고리즘/JAVA] 백트래킹(Backtracking) : 개념 (N-Queen / 스도쿠) (0) | 2024.04.16 |
| [자료구조/JAVA] 해시 테이블 (Hash Table) (0) | 2024.03.31 |
| [자료구조/JAVA] 허프만 코딩 (Huffman Coding) (0) | 2024.03.31 |
| [자료구조/JAVA] 우선순위 큐 : 힙(Heap) (0) | 2024.03.28 |













