[알고리즘/JAVA] 그리디 (Greedy) : 개념 (동전, 단어 수학, 허프만 코딩)

그리디 알고리즘 (Greedy)
나는 미래를 위해서 지금 어떤 행동을 해야 가장 효율적일지 모른다. 하지만 눈앞에 보이는 상황에서 현재의 최선을 다하려고 한다.
그리고 이것은 그리디 알고리즘을 설명하는 말이다.
그리디 알고리즘은 매번의 선택의 순간에서의 최선인 답을 도출하면서 결과를 도출하는 방법이다.
해당 방법은 매 순간에서는 최선일 수 있고 적당히 좋은 값을 찾는 것이 목표이지, 전체적으로 보았을 때에는 항상 최적이라는 보장이 없다.
그리디의 최적 조건
그리디가 항상 최적해를 보장하지 못한다고 하였다. 따라서 그리디를 이용하여 최적해를 구해야 하는 경우에 따져봐야 하는 조건이 있다.
1. 탐욕적 선택 속성: 앞의 선택이 이후의 선택에 영향을 미쳐서는 안 된다.
2. 최적 부분 구조: 작은 부분 문제의 최적 해를 이용해 전체 문제의 최적 해를 구할 수 있어야 한다.
다음의 경우로 한번 생각을 해보자.
점심밥을 해결하기 위해서 식사류 한 종류와, 음료 한 종류를 선택해서 끼니를 때우려고 한다. 그렇지만 나는 돈이 없어서 최대한 저렴하게 먹어야 한다.
- 식사류 : 패스트푸드(8000원), 한식(10000원)
- 음료류 : 생수(500원), 보리차(2000원), 콜라(3000원), 아메리카노(4000원)
1. 식사류와 음료류를 자유롭게 한 개씩 고를 수 있는 경우
- 해당 경우 탐욕적 방법으로 패스트푸드와 생수를 선택하는 것, 각각의 선택에서 탐욕적 선택을 하는 것이 최적해이다.
2. 식사류에 따라 음료의 선택이 한정되는 경우
- 패스트푸드를 선택했다면 콜라와 아메리카노만을 선택할 수 있다고 가정해보자. (햄버거와 보리차는 안어울린다)
- 그렇다면 탐욕적으로 패스트푸드를 골라도 결국 최적해가 될 수 없다.
- 해당 경우는 이전 선택의 결과가 이후 선택에 영향을 주므로, 각 단계에서의 최적 선택이 전체적으로 최적의 해를 보장할 수 없다.
언제 사용해야 하는가?
1. 최적해 보장 : 위 두가지의 조건이 성립하지 않는다면 그리디 알고리즘으로는 최적해를 구할 수 없다. 따라서 최적의 결과를 구해야 하는 문제라면 조건이 성립하는 지를 판단해야 한다.
이 때문에 그리디를 사용하는 PS 문제들은 비교적 해당 판단을 쉽게 내릴 수 있도록 문제를 내는 편이며, 여러가지 제약 조건이 많이 걸린 문제에서 그리디를 활용할 수 있을 확률이 높다. (아래에서 나올 거스름돈 문제에서 동전의 종류가 제약되는 등..)
- 둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)
2. 적당한 결과 : 그럼에도 불구하고 그리디 알고리즘은 대부분 어느정도 괜찮은 퍼포먼스를 보여주는 경우가 많다. 따라서 최적이 아니더라도, 어떻게든 결과만 맞게 나오면 되는 경우라면 그리디를 사용해도 된다.
3. 근사치 : 그리디로 적당히 나온 결과를 기준으로 복잡한 알고리즘에서의 역할을 할 수도 있다. 예를 들어 백트래킹 알고리즘에서 유망성을 판단하는 데에 역할을 하는 등, 다른 알고리즘에서의 최소 커트라인으로서 역할을 할 수 있다.
거스름돈 문제
어떻게 해야 거스름돈의 동전의 개수를 최대한 적게 드릴 수 있는가? 가장 많이 알려진 그리디 문제이다.
거스름돈 문제로 위의 관점을 다시 되새겨보자.
1. 우리나라 동전의 종류에는 10원, 50원, 100원, 500원이 있다. 일상생활에서 우리가 손님에게 거스름돈을 드릴 때, 가장 액수가 큰 화폐를 최대한 많이 드린다.
- 만약 1100원을 거슬러 드려야 한다면 그리디한 방식으로 500원 2개, 100원 1개로 총 3개의 동전을 사용하면 되고, 이것은 최적의 해이다.
2. 만약 700원짜리 동전이 새로 발행됬다고 생각해보자.
- 만약 똑같이 그리디한 방식을 사용한다면 1100원을 거슬러 드리는 방법은 700원 1개, 100원 4개를 사용하여 총 5개의 동전을 사용해야 한다. 하지만 이는 앞에서 도출해낸 총 3개의 동전을 사용하는 방법이 있으므로 최적해가 아니다.
첫 번째 예시에서는 그리디 선택이 가능하다. 매 단계에서 가장 큰 화폐 단위부터 거스름돈을 최대한 많이 주는 것, 탐욕적인 선택이 최적의 해가 된다.
하지만 두 번째 예시에서는 그리디 알고리즘으로 해결할 수 없다. 새로운 동전이 추가되면서 가장 큰 화폐 단위부터 선택한다고 해도 전체적으로 최적의 해를 보장할 수 없다는 것은 최적 부분 구조가 파괴되기 때문이다.
여담으로 거스름돈 문제의 그리디로 풀이 시 최적해가 나오는 조건은 동전이 배수의 관계를 유지할 때 이다.
문제 : 동전 0 (백준 11047)
위에서 설명한 문제이다. 아래와 같은 입력 조건이 있다. 이는 위에서 살펴본 그리디로 최적해를 보장할 수 있는 경우에 해당한다.
"둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)"
따라서 가장 큰 동전부터 총 금액에서 나누고, 나머지에 대해서 다음으로 가치가 큰 동전으로 나누고..를 반복하면 된다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Integer[] money = new Integer[n];
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
money[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(money, Collections.reverseOrder());
int count = 0;
for(int m : money){
count += k / m;
k = k % m;
if(k == 0){
break;
}
}
System.out.println(count);
}
}
그리디를 사용할 수 없는 문제 : 동전 2 (백준 2294)
위의 문제와 유사해 보이는 경우이지만. 아쉽게도 최소값, 즉 최적해를 구하는 문제이고 제약 조건이 그리디를 사용하기 적합하지 않은 문제이다.
동전의 종류가 정해져 있지 않으므로 아까 말했던 700원짜리 동전이 추가되는 경우, 동전이 배수를 이루지 못해서 최적해를 구하지 못하는 것을 생각하면 된다.
따라서 해당 경우는 부분해간의 점화식을 세워서 다이나믹 프로그래밍으로 풀이하는 등 다른 방법을 사용했다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] values = new int[n+1];
for(int i = 1; i <= n; i++){
st = new StringTokenizer(br.readLine());
values[i] = Integer.parseInt(st.nextToken());
}
int[][] dp = new int[n+1][k+1];
Arrays.sort(values);
for(int i = 1; i <= k; i++){
dp[0][i] = 100001;
}
for(int i = 1; i <= n; i++){ // 동전의 종류
for(int j = 1; j <= k; j++){ // k = 총 금액
if(j - values[i] < 0){
dp[i][j] = dp[i-1][j]; //해당 동전을 포함시킬 수 없는 경우 이전 최적해 사용
}
else{
// 동전을 포함시킬 수 있는 경우 이전 최적해 vs 포함시켰을 경우 해
// 만약 i번째 동전인 5원을 포함시키는 경우 k=21일 때를 계산한다면 "dp[i][16] + 1" 이 포함시켰을 경우의 해이다.
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-values[i]] + 1);
}
}
}
if(dp[n][k] == 100001){
System.out.println(-1);
}
else{
System.out.println(dp[n][k]);
}
}
}
DP를 설명하는 포스팅은 아니므로 코드와 주석만 남기고 넘어가도록 하겠다.
문제 : 단어 수학 (백준 1339)
위 문제도 탐욕적인 방법으로 최적해를 구할 수 있다는 것을 직관적으로 알 수 있다.
그래도 그리디 관점으로 설명해보면, 각 알파벳이 나타내는 수를 선택할 때, 가장 가치가 높은 알파벳부터 높은 수를 부여하면 된다.
그렇다면 가치가 높은 알파벳이라는 것은 무엇일까? 높은 자리 수에 많이 등장하는 알파벳이 될 것이다.
1. 알파벳의 가치를 아래의 예시로 매겨보도록 하자.
- GCF, ACDEB
2. 만약 모든 알파벳에 1을 부여한다면 아래와 같은 가치가 나올 것이다.
- A : 10000
- C : 1010
- G : 100
- D : 100
- E : 10
- B : 1
- F : 1
3. 따라서 A부터 B까지 차례로 수를 부여하면 아래와 같다.
- A(9) : 10000 -> 90000
- C(8) : 1010 -> 8080
- G(7) : 100 -> 700
- D(6) : 100 -> 600
- E(5) : 10 -> 50
- B(4) : 1 -> 4
- F(3) : 1 -> 3
4. 모든 수를 합하면 결과가 나온다.
- 99437
구현
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
// 단어의 가치 계산
Map<Character, Integer> map = new HashMap<>();
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
char[] chs = st.nextToken().toCharArray();
for(int j = 0; j < chs.length; j++){
char c = chs[j];
int num = (int)Math.pow(10, chs.length - 1 - j);
if(map.containsKey(c)){
map.replace(c, map.get(c) + num);
}
else{
map.put(c, num);
}
}
}
// 단어를 가치가 높은 순으로 정렬
List<Integer> list = new ArrayList<>();
for(char ch : map.keySet()){
list.add(map.get(ch));
}
Collections.sort(list, Collections.reverseOrder());
// 가치가 높은 수부터 숫자 부여 후 연산
int k = 9;
int result = 0;
for(int i = 0; i < list.size(); i++){
result += (list.get(i) * k);
k--;
}
System.out.println(result);
}
}
사례 : 허프만 코딩
웬지 위의 문제를 풀다가 허프만 코딩이 생각났다면 정상이다. 허프만 코딩도 사실 그리디 알고리즘의 예시이기 때문이다.
허프만 코딩은 각 문자를 나타내는 코드의 길이를 최소화하기 위해 빈도가 높은 문자에 더 짧은 코드를 할당하는 그리디한 접근을 사용한다.
이를 위해서 허프만 트리를 구성하게 되는데, 이 때 힙을 구성하는 방법을 간단히 나타내면 아래와 같다.
1. 빈도수가 낮은 노드를 우선순위 큐에서 두 개를 꺼내서 묶는다.
2. 해당 빈도수를 합한 노드를 다시 우선순위 큐에 넣는다.
3. 다시 우선순위 큐에서 두 개를 꺼내서 묶는다.
4. 이를 하나의 노드만 남을 때 까지, 즉 모두 트리로 구성될 때 까지 반복한다.
해당 과정은 빈도수가 낮은 문자에 대해서는 트리의 깊은 곳에, 빈도수가 높은 문자에 대해서는 트리의 위쪽에 위치하도록 하기 위해 탐욕적으로 지금 당장 빈도수가 가장 낮은 노드 두 개를 선택하는 것을 반복했으며, 이에 기반해서 빈도수가 많은 문자에 짧은 부호를 부여하는 그리디한 벙식이다.
함께 보기 : 허프만 트리
허프만 트리는 빈도 수를 우선순위로 하는 우선순위 큐(최소 힙)을 구성하게 된다.
해당 힙에서 빈도가 가장 낮은 두 문자를 선택하여 하나의 부모 노드를 가진 허프만 트리를 만든다.
부모 노드의 빈도는 자식 노드 빈도의 합으로 설정하고 모든 문자가 하나의 트리로 합쳐질 때까지 반복한다.
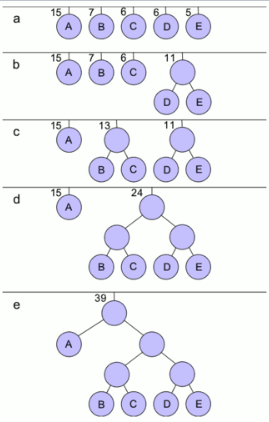
1. 빈도수로 최소 힙을 생성한다.
2. 빈도수가 가장 낮은 두 문자를 선택하여 트리로 묶는다.
(D와 E가 6, 5 이므로 부모 노드의 빈도는 11로 설정된다.)
3. 다시 빈도수가 가장 낮은 두 문자를 선택하여 트리로 묶는다.
(15(A), 7(B), 6(C), 11(D,E) 중 가장 낮은 빈도수인 B,C를 묶는다.)
4. 마찬가지로 15(A), 13(B,C), 11(D,E) 중 가장 낮은 빈도수인 (B,C), (D,E)를 묶는다.
5. 마지막으로 15(A), 24(B,C,D,E)를 묶어 허프만 트리의 생성을 완료한다.
https://sjh9708.tistory.com/207
[자료구조/JAVA] 허프만 코딩 (Huffman Coding)
허프만 코딩 데이터 문자의 등장 빈도에 따라 다른 길이의 부호를 사용하여 데이터를 압축하는 알고리즘이다. 자주 등장하는 문자는 짧은 부호로, 드물게 등장하는 문자는 긴 부호로 표현하여
sjh9708.tistory.com
그리디와 우선순위 큐
그리디 문제에서는 심심치 않게 우선순위 큐를 함께 사용하는 유형들이 많이 등장한다.
그리디 알고리즘은 매번의 선택의 순간에서의 최선인 답을 도출하면서 결과를 도출하는 방법이다. 매 순간에 최선의 해답을 판단해야 할 때, 우선순위 큐가 유용하게 사용될 수 있다.
우선순위 큐는 그리디에서 매 순간의 최적의 선택이 이전의 결정에 의해 영향을 받을 경우, 그 선택의 후보군들을 저장해 둘 수단으로서 유용하게 사용될 수 있다.
https://sjh9708.tistory.com/220
[알고리즘/JAVA] 그리디와 우선순위 큐 (과제, 강의실 배정, 보석 도둑)
그리디와 우선순위 큐 그리디 알고리즘은 매번의 선택의 순간에서의 최선인 답을 도출하면서 결과를 도출하는 방법이다. 매 순간에 최선의 해답을 판단해야 할 때, 우선순위 큐가 유용하게 사
sjh9708.tistory.com
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 이진 탐색 : 개념 (수 찾기, 랜선 자르기) - Upper/Lower Bound (0) | 2024.05.06 |
|---|---|
| [알고리즘/JAVA] 분할 정복법 : 개념 (합병 정렬, 행렬 제곱, 색종이) (0) | 2024.05.05 |
| [알고리즘/JAVA] 동적 계획법(DP) : LIS (최장 증가 부분 수열) (0) | 2024.05.01 |
| [알고리즘/JAVA] 동적 계획법(DP) : 배낭 채우기 문제 (0-1 Knapsack) (0) | 2024.04.30 |
| [알고리즘/JAVA] 누적 합 (Prefix Sum) (0) | 2024.04.20 |













