[알고리즘/JAVA] 누적 합 (Prefix Sum)

누적합 (Prefix Sum)
배열 또는 리스트 등에서 일정 구간의 합을 빠르게 계산하기 위한 방법이면서 동적 계획법(DP)의 형태 중 하나이다.
기본적인 방식은 각 요소까지의 누적 합을 계산하여 이를 배열에 저장해 두는 것이다. 이후에 특정 구간의 합을 구할 때는 해당 구간의 끝 지점까지의 누적 합에서 시작 지점까지의 누적 합을 빼는 것이다.
해당 알고리즘은 배열 또는 리스트의 요소가 고정되어 있을 때 구간 합을 반복적으로 계산해야 하는 경우 유용하게 사용될 수 있다.
1차원 배열의 누적합 (백준 11659)
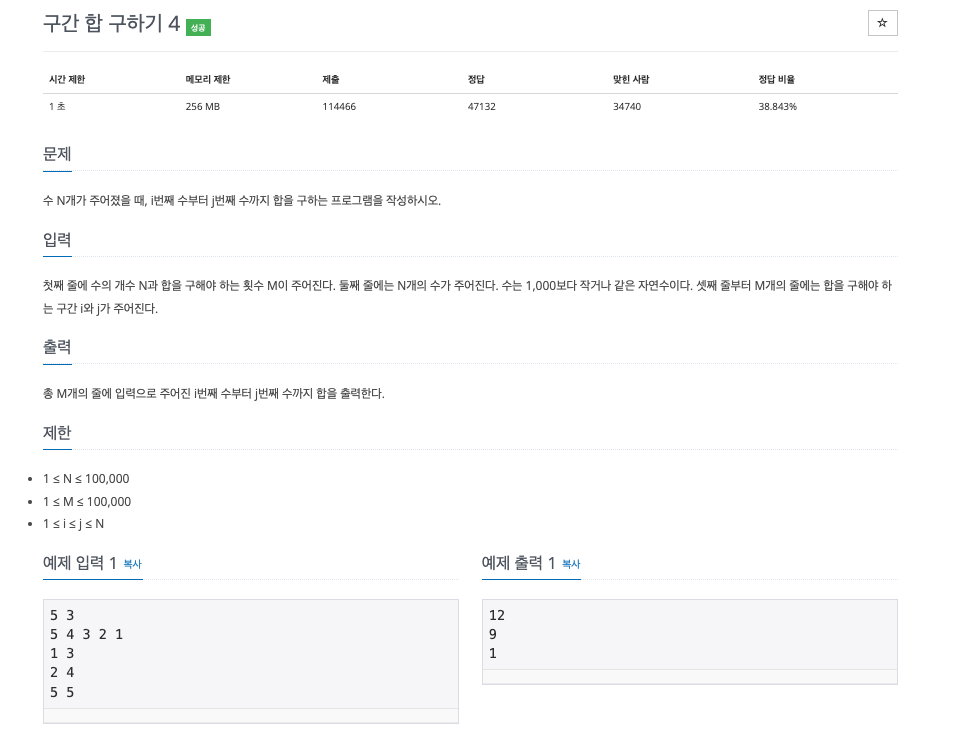
다음 문제를 보면, 1차원 배열이 주어지며, 그 이후로 주어지는 시작 인덱스와 마지막 인덱스의 쌍에 대해서 그 구간의 합을 구하는 문제이다.
진짜 단순하게 각 입력에 대해서 일일이 반복문을 돌려서 계산하면 되는 것이 아닌가 생각할 수 있다.
그렇지만 배열의 원소 개수 N과, 케이스 개수 M을 보면, 해당 방식으로 문제를 풀이할 시 최악의 경우 10만 * 10만의 연산이 이루어지며, 이는 1초 시간제한에 의해서 시간초과가 날 것이다(보통 1초 시간제한은 1억개 연산보다 아래로 풀이되게 된다.)
따라서 누적합 알고리즘에 의한 풀이를 고려해야 한다.
| 5 | 4 | 3 | 2 | 1 |
해당 배열에서 각각에 입력에 대한 풀이는 다음과 같다.
- (1, 3) -> 5 + 4 + 3 = 12
- (2, 4) -> 4 + 3 + 2 = 9
- (5, 5) -> 1
하지만 다르게 생각하면 이렇게 볼 수도 있다.
- (1, 3) -> (1, 3)
- (2, 4) -> (1, 4) - (1, 1) -> 14 - 5 = 9
- (5, 5) -> (1, 5) - (1, 4) -> 15 - 14 = 1
즉 맨 처음부터 해당 인덱스까지의 누적합을 계산해두면, 임의의 구간에 대한 풀이를 해당 누적합을 이용해서 풀이할 수 있다는 것이다.
누적합 수식
원래 배열 (A)
| - | 1 | 2 | 3 | 4 | 5 |
누적합 배열 (B)
| 0 | 1 | 3 | 6 | 10 | 15 |
누적합 구하기 : 다음과 같이 원래 배열을 누적합 배열로 표현할 수 있다. 누적합 배열 B(i)의 식은 다음과 같이 표현된다.
- B(i) = B(i-1) + A(i) (i > 1)
위의 수식에 따라서 원래 배열의 앞쪽 인덱스 하나를 0으로 비워둔 채로 풀이하면 원래 배열의 모든 원소에 대해서 해당 식을 적용할 수 있다.
구간합 구하기 : 구간 [start, end]의 구간합을 구하려면 아래와 같이 표현된다.
- 구간합 [start : end] = B(end) - B(start - 1)
구현
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static long[] numbers;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
numbers = new long[n + 1];
st = new StringTokenizer(br.readLine());
// 배열에 누적 합 형태로 입력 받기
for(int i = 1; i <= n; i++){
numbers[i] = numbers[i-1] + Long.parseLong(st.nextToken());
}
// 구간 합 구하기
StringBuilder sb = new StringBuilder();
for(int i = 1; i <= m; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
long result = numbers[end] - numbers[start - 1];
sb.append(result).append("\n");
}
System.out.println(sb);
}
}
2차원 배열의 누적합 (백준 11660)
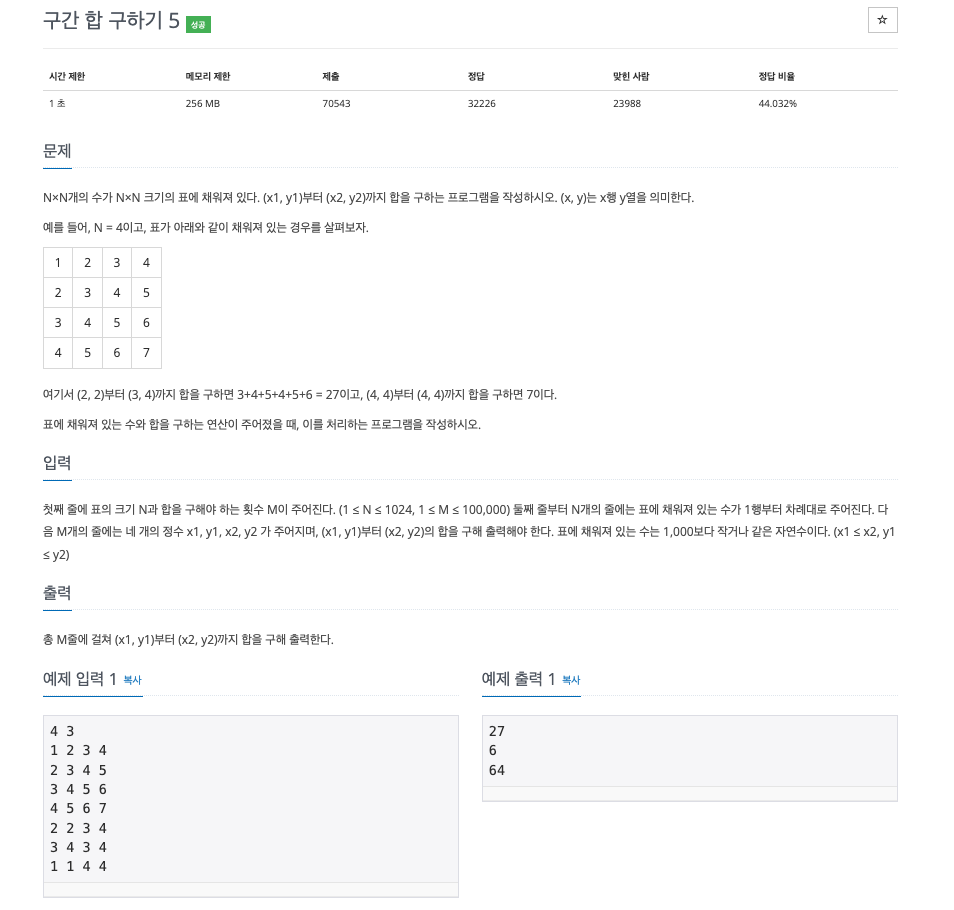
이번에는 2차원 배열에서의 구간 합을 누적합을 사용해서 구해볼 것이다.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
먼저 일반적으로 원래 배열 A에서 (2, 2)부터 (3, 3)까지의 합을 구한다고 치면 아래와 같을 것이다.
- 3 + 4 + 4 + 5 = 16
누적합 배열로의 표현
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 3 | 6 | 10 |
| 0 | 3 | 8 | 15 | 24 |
| 0 | 6 | 15 | 27 | 42 |
| 0 | 10 | 24 | 42 | 64 |
해당 누적합 배열 B는 (1, 1)부터 (x, y)까지의 누적합에 대해서 표현한 배열이다. 예를 들어 누적합 배열(3, 3)는 아래와 같다.
- B(3, 3) = A(1, 1) + A(1, 2) + A(1, 3) + A(2, 1) + A(2, 2) + A(2, 3) + A(3, 1) + A(3, 2) + A(3, 3)
= 1 + 2 + 3 + 2 + 3 + 4 + 3 + 4 + 5 = 27
원래 배열을 살펴보면서 누적합에 대한 규칙을 살펴보자. 누적합은 이전의 누적합 + 현재 배열의 수치라는 원리를 가지고 있다.
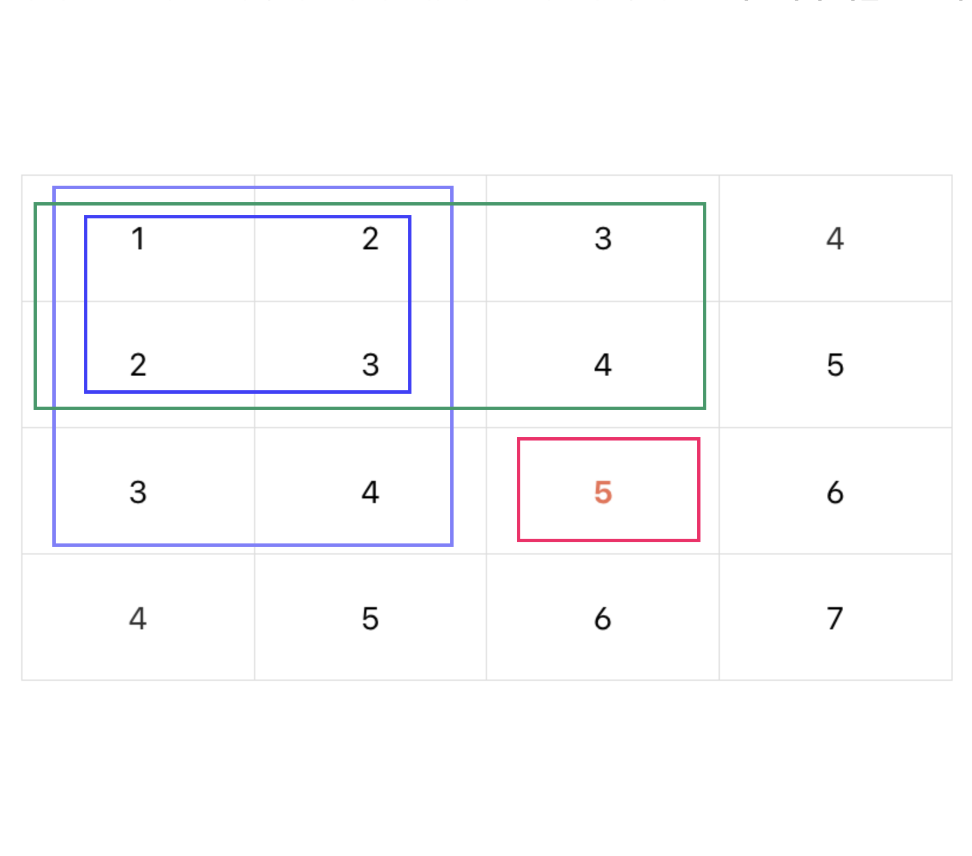
B(3,3) = 27은 위의 원래 배열에서의 네 개의 박스로 표현이 가능하다.
- 초록색 박스(15) + 연보라색 박스(15) - 파란색 박스(8) + 빨간색 박스(5) = 누적합 27
그리고 해당 박스들은 곧 누적합으로 표현이 가능하다.
- 초록색 박스 : B(2, 3)
- 연보라색 박스 : B(3, 2)
- 파란색 박스 : B(2, 2)
- 빨간색 박스 : A(3, 3)
즉 위쪽 누적합의 합 + 왼쪽 누적합의 합에서 두 번 연산된 공통된 누적합을 한 번 뺄셈하여 한번만 연산되게 한 값이 이전 누적합이 될 것이고, 이전 누적합과 현재 배열의 수치를 합해서 현재 인덱스의 누적합을 만들 수 있는 것이다.
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 3 | 6 | 10 |
| 0 | 3 | 8 | 15 | 24 |
| 0 | 6 | 15 | 27 | 42 |
| 0 | 10 | 24 | 42 | 64 |
B(3, 3)의 누적합 27은 15 + 15 - 8 + 5로 계산된다는 것을 다시한번 확인해보자.
구간합 구하기
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 3 | 6 | 10 |
| 0 | 3 | 8 | 15 | 24 |
| 0 | 6 | 15 | 27 | 42 |
| 0 | 10 | 24 | 42 | 64 |
만약 위에서 계산했던 누적합 테이블을 사용해서 [(3:3) : (3:3)]의 구간합을 계산하려면 어떻게 해야 할까?
[(1, 1) : (3, 3)]까지의 누적합을 만들 때 15+15-8+5 로 계산되었었다. [(3:3) : (3:3)]의 구간합은 원래 배열의 수치 5에 해당한다. 따라서 해당 수식을 역으로 원상복귀 시켜주면 일반식을 얻을 수 있다.
- 27 - 15 - 15 + 8 = 5
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 3 | 6 | 10 |
| 0 | 3 | 8 | 15 | 24 |
| 0 | 6 | 15 | 27 | 42 |
| 0 | 10 | 24 | 42 | 64 |
[(2:2) : (3:3)]의 구간합의 경우로도 생각해보자. 정답부터 말하자면 16(3+4+4+5)이다.
이를 위해서 도출해낸 식으로 계산해보면 같은 결과를 얻을 수 있다.
- 27 - 6 - 6 + 1 = 16
구간합 [(x1 ,y1) : (x2, y2)] = B(x2, y2) - B((x1 - 1), y2) - B(x2, (y1 - 1)) + B((x1 - 1), (y1 - 1))
구현
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int n;
static int m;
static int[][] array;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
//원본 크기보다 1씩 큰 2차원 배열
array = new int[n+1][n+1];
for(int i = 1; i <= n; i++){
st = new StringTokenizer(br.readLine());
for(int j = 1; j <= n; j++){
// 누적합 배열 표현
array[i][j] = array[i-1][j] + array[i][j-1] - array[i-1][j-1] + Integer.parseInt(st.nextToken());
}
}
for(int[] l : array){
System.out.println(Arrays.toString(l));
}
StringBuilder sb = new StringBuilder();
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int y1 = Integer.parseInt(st.nextToken());
int x1 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
// 구간합 계산
int sum = array[y2][x2] - array[y1-1][x2] - array[y2][x1-1] + array[y1-1][x1-1];
sb.append(sum).append("\n");
}
System.out.println(sb);
}
}
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [알고리즘/JAVA] 동적 계획법(DP) : LIS (최장 증가 부분 수열) (0) | 2024.05.01 |
|---|---|
| [알고리즘/JAVA] 동적 계획법(DP) : 배낭 채우기 문제 (0-1 Knapsack) (0) | 2024.04.30 |
| [알고리즘/JAVA] 동적 계획법(DP) : 개념 (파도반 수열 / 1로 만들기 / 계단 오르기) (0) | 2024.04.16 |
| [알고리즘/JAVA] 백트래킹(Backtracking) : 개념 (N-Queen / 스도쿠) (0) | 2024.04.16 |
| [알고리즘/JAVA] 정렬 알고리즘 : 선택, 삽입, 버블, 병합, 퀵 정렬 (0) | 2024.04.05 |













