[알고리즘/JAVA] 재귀와 반복 : 등차수열, 피보나치, 팩토리얼, 하노이탑
재귀와 반복(Recursion, Iteration)
재귀
- 자신을 호출함으로써 문제를 해결하는 방식.
- 문제를 부분 문제로 나누고.,부분 문제에 대해 동일한 알고리즘을 사용하여 해결하는 분할 정복법의 일종
- 종료 조건을 만족할 때까지 자신을 호출한다.
- 함수 호출 스택에 추가 비용이 들어가기 때문에 과도한 재귀 호출은 스택 오버플로우를 유발할 수 있다.
- Top-down 방식은 주로 재귀적인 접근 방식을 사용하며, 문제를 작은 문제로 쪼개고 결합하여 전체 문제의 해를 구한다.
반복
- 반복문을 사용하여 문제를 해결하는 방법
- 코드가 좀 더 복잡할 수 있으나, 스택 오버플로우 문제에 상대적으로 자유롭다.
- Bottom-up 방식은 주로 반복적인 방식을 사용하고, 먼저 작은 문제를 해결하고 이를 이용해서 더 큰 부분 문제들을 점진적으로 해결해 나가는 방식이다.
문제 1 : 등차수열
해당 문제는 첫 항이 1이고, v = 공차일 때, 등차수열의 n번째 항을 구하는 문제이다.
예를 들어 n = 5, v = 3 일 때, 1, 4, 7, 10 ,13이므로 답으로 13이 나와야 한다.
재귀적 방법
int recursiveSeq(int n, int v){
if(n == 1){
return 1;
}
else{
return recursiveSeq(n - 1, v) + v;
}
}
n이 1인 경우: 첫 번째 항이므로 항상 1을 반환한다.
나머지 경우: 재귀적으로 n-1번째 항을 계산한 후 v를 더하여 반환한다. 이전 항에 v를 더한 값을 현재 항으로 설정하는 것이다.
recursiveSeq(5, 3) = recursiveSeq(4, 3) + 3
recursiveSeq(4, 3) = recursiveSeq(3, 3) + 3
recursiveSeq(3, 3) = recursiveSeq(2, 3) + 3
recursiveSeq(2, 3) = recursiveSeq(1, 3) + 3
recursiveSeq(1, 3) = 1
n=5, v=3일 때의 호출 과정은 다음과 같다.
반복적 방법
int iterativeSeq(int n, int v){
int result = 1;
for(int i = 2; i <= n; i++){
result += v;
}
return result;
}result = 1
i = 2: result = result + 3 = 1 + 3 = 4
i = 3: result = result + 3 = 4 + 3 = 7
i = 4: result = result + 3 = 7 + 3 = 10
i = 5: result = result + 3 = 10 + 3 = 13
해당 방법은 반복적으로 풀이했을 때의 과정이다.
문제 2 : 피보나치 수열
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
각 항은 이전 두 항의 합이다. 첫번째 항과 두번째 항은 1이며, n번째 항은 (n-1)번째 항과 (n-2)번째 항의 합이다.
n번째 항을 구하는 것이 문제이다.
반복적 방법
int iterativeFib(int n){
int prev = 1;
int current = 1;
for(int i = 3; i <= n; i++){
int tmp = prev + current;
prev = current;
current = tmp;
}
return current;
}
반복문을 사용하여 피보나치 수열의 n번째 항을 계산한다.
초기 값으로 첫 번째와 두 번째 항을 1로 설정하고, 세 번째 항부터 n번째 항까지 반복문을 통해 계산한다.
반복문 내부에서는 현재 항과 그 전 항의 값을 더하여 다음 항을 계산하고 해당 값을 이전 항의 값으로 업데이트하는 과정을 n번째 항까지 반복하여 최종 결과를 반환하게 된다.
재귀적 방법
int recursiveFib(int n){
if(n <= 1){
return n;
}
else{
return recursiveFib(n - 1) + recursiveFib(n - 2);
}
}- n=4일 때, recursiveFib(4)를 호출하면 n이 4이므로 두 번째 else 절이 실행된다.
- recursiveFib(3)과 recursiveFib(2)를 각각 재귀적으로 호출한다.
- 계속해서 재귀 호출이 이루어지다가, n이 1 또는 0이 될 때까지 호출이 진행된다.
- 반환된 값들이 이전 호출로 되돌아가며 더해지는 과정이 이루어진다.
recursiveFib(4)
├─ recursiveFib(3)
│ ├─ recursiveFib(2)
│ │ ├─ recursiveFib(1)
│ │ │ └─ return 1
│ │ └─ recursiveFib(0)
│ │ └─ return 0
│ └─ recursiveFib(1)
│ └─ return 1
└─ recursiveFib(2)
├─ recursiveFib(1)
│ └─ return 1
└─ recursiveFib(0)
└─ return 0
재귀적인 방식으로 피보나치 수열을 계산할 때, 동일한 값을 반복해서 계산하게 되는 것을 볼 수 있다. fib(4)를 계산할 때 fib(2)을 두 번 호출하게 되고, fib(1)을 세 번 호출해야 하는 것을 볼 수 있다.
또한 메모리에 계속해서 호출 정보가 쌓이게 되는데, 피보나치 수열의 경우 재귀 호출의 깊이가 매우 깊어지게 되면 메모리에 엄청난 량의 호출 스택이 쌓이게 된다. 따라서 스택 메모리를 초과하여 스택 오버플로우가 발생할 수 있다.
55
재귀 : 걸린 시간 118708
55
반복 : 걸린 시간 10917
55
재귀 리팩토링 : 걸린 시간 35000
n=10인 경우, 실제로 두 경우의 시간을 측정해보면, 재귀가 반복에 비해서 훨씬 많은 시간을 소요하게 된다.
실제로 n=100이 되는 경우 재귀호출 시 3만 5천년 정도의 시간이 소요된다고 한다.
성능 개선 : 동적 프로그래밍
Map mem = new HashMap<Integer, Integer>();
int recursiveFibDp(int n){
if(n <= 1){
return n;
}
else{
if(mem.containsKey(n)){
return (int)mem.get(n);
}
int res = recursiveFib(n - 1) + recursiveFib(n - 2);
mem.put(n, res);
return res;
}
}
위에서 동일한 값을 계산하는 함수를 중복해서 호출하는 것이 문제점 중 하나였다. 해당 문제를 개선하기 위해서 계산이 완료되어 값을 도출한 함수를 변수에 저장해두고, 나중에 해당 변수에 값이 존재한다면 계산을 또 다시 하는 대신 해당 값을 사용하도록 할 수 있다.
이러한 메모리제이션 기법을 동적 프로그래밍(DP)라고 부르며, 중복 계산을 회피하기 위한 전략으로 사용한다.
55
재귀 : 걸린 시간 118708
55
반복 : 걸린 시간 10917
55
재귀 리팩토링 : 걸린 시간 35000
문제 3 : 팩토리얼
5! = 5 * 4 * 3 * 2 * 1이다.
N에 대한 팩토리얼 값을 구하는 문제이다.
int recursiveFactorial(int n){
if(n == 1){
return n;
}
return n * recursiveFactorial(n - 1);
}
int iterativeFactorial(int n){
int current = 1;
for(int i = 2; i <= n; i++){
current *= i;
}
return current;
}
위와 마찬가지로 재귀적인 방법과, 반복적인 방법으로 풀 수 있다.
문제 4 : 하노이 탑
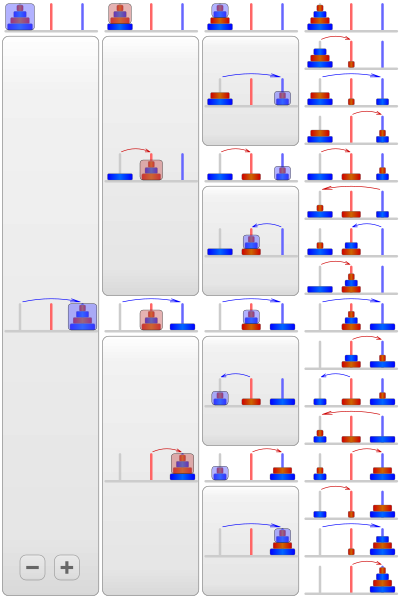
세 개의 기둥과 이 기둥에 꽂을 수 있는 서로 다른 크기의 원반들이 있다. 각 기둥은 출발지, 도착지, 보조 기둥이며 출발지에서 도착지까지 모든 원반을 이동시키는 것이 목표이다.
<규칙>
작은 원반 위에 큰 원반이 올라가지 않는다.
한 번에 하나의 원반만 이동할 수 있다.
왼쪽의 그림은 4개의 원반을 도착지로 이동시키는 과정이며, 해당 과정은 오른쪽으로 갈 수록 부분 문제를 해결하여 결과로 결합하는 과정이다.
왼쪽에서부터 1번째, 2번째 그림이 가장 아래에 깔려 있는 원반을 목표 지점으로 옮기는 과정이며, 해당 과정은 다음과 같이 이루어진다.
1. 가장 큰 원반을 제외한 나머지 기둥을 보조 기둥으로 옮긴다.
2. 가장 큰 원반을 도착지로 옮긴다.
3. 보조 기둥에 있는 나머지 기둥을 도착지로 옮긴다.
void hanoi(int n, String source, String dest, String temp){
if(n == 1){
System.out.println("N : " + n + " , Move : " + source + "->" + dest);
return;
}
hanoi(n - 1, source, temp, dest); // Source -> Temp
System.out.println("N : " + n + " , Move : " + source + "->" + dest);
hanoi(n - 1, temp, dest, source); // Temp -> Dest
}
n: 원반의 수, source: 출발 기둥, dest: 목표 기둥, temp: 보조 기둥
source, dest, temp를 각각 A, C, B라고 하자.
n이 1인 경우: 원반 한 개를 옮기는 작업이므로 이동 경로를 출력하고 함수를 종료한다.
1. 재귀적으로 n-1개의 원반을 A에서 B로 옮긴다. (n-1개의 보조 기둥에 대해서 출발 기둥이 A이고 목표 기둥이 B인 함수가 내부적으로 호출)
2. 남은 하나의 큰 원반을 A에서 C로 옮긴다
3. B의 원반에 대해서도 C로 옮긴다. (n-1개의 보조 기둥에 대해서 출발 기둥이 B이고 목표 기둥이 C인 함수가 내부적으로 호출)
해당 과정을 재귀적으로 반복하여 부분 문제를 해결하여 하노이 탑 문제를 풀어낼 수 있다.
N : 1 , Move : A->C
N : 2 , Move : A->B
N : 1 , Move : C->B
N : 3 , Move : A->C
N : 1 , Move : B->A
N : 2 , Move : B->C
N : 1 , Move : A->C
'PS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조/JAVA] 트리 (1) : 이진 트리(Binary Tree) : 순회 및 연산 (0) | 2024.03.19 |
|---|---|
| [자료구조/JAVA] 연결 리스트(Linked List) (0) | 2024.03.13 |
| [자료구조/JAVA] 동적 배열(Dynamic Array) 구현 (1) | 2024.03.12 |
| [자료구조/JAVA] 스택과 큐(Stack, Queue) (0) | 2024.03.11 |
| [알고리즘] 시간 복잡도와 코딩 테스트 (0) | 2023.07.05 |














